求极限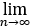 
sin(k/n)∙sin(k/n²)
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
求极限 (sinx-arctanx)/(tanx-arcsinx)
设二元函数f(x,y)在(x0,y0)的某邻域U内有定义，且在U内存在偏导数.证明：若偏导数fx(x,y)和fy(x,y)都在(x0,y0)可微，则fxy (x0,y0 )=fyx (x0,y0).
设f(x)在(-∞,+∞)上可导，且对任意实数x有f(x)=f(x+2k)=f(x+b)，其中k为正整数，b为正无理数，用Fourier级数理论证明f(x)为常数.
设f:[0,1]→(0,+∞)为连续函数，常数a≥1.证明：=a+1.
设α,β是任意非零实数，对正整数n，证明： =其中=α(α-1)⋯(α-k+1)/k!,=1.
(1)证明：方程(x+1)x+1=exx有唯一正根.(2)若β为(1)中方程的根，计算极限(β+1/n)(β+2/n)⋯(β+n/n).
设I(x0,x1 )=∬Σ/dydz，其中Σ为抛物面x=y²+z²与平面x=x0,x=x1所围立体表面的内侧，α>0,x1>x0>0，求极限I(x0,x1).
已知正项级数an 收敛，数列{xn}满足|xn+1-xn |≤a_n,∀n≥1.证明：{xn}收敛.
设数列{xn}满足xmn≤xm+xn,xn>0，证明：存在.
设x1=1,xn+1=,n=1,2,3,⋯(1)证明：xn =0.(2)计算n(xn-ln(1+xn)).
设函数f,g在[0,1]上连续，且存在包含于[0,1] 的数列{xn}，使得对于任意n≥1，有f(xn)= g(xn+1).证明：存在ξ∈[0,1],使得 f(ξ)=g(ξ).
求极限：n[(1²+3²+⋯+(2n+1)²)/n³ -4/3]
设数列{xn}有界，且(xn+1-xn)=0，令 m=xn ,M=xn,m<M证明：在区间(m,M)上任意一个数都是此数列的一个子列的极限.
(1/(ex-1)-1/ln(1+x) )=______.
设y=y(x)由方程y²-x+siny=0(x≥1)确定，且y=y(x)经过(π²,π).试讨论y(x)在(1,+∞)上零点的个数，并求y(x).
设f(x)在[a,b)上严格单调，xn∈(a,b)，证明：如果f(xn)=f(a)，则xn=a.
设f(x),g(x)在(-∞,+∞)上连续，且[f(x)-g(x)]=0.证明：f(x)在(-∞,+∞)上一致连续当且仅当g(x)在(-∞,+∞)上一致连续.
函数f(x)=|x|1/(1-x)(x-2)的第一类间断点的个数是【 】
若((1+ax²)sinx-1)/x³=6，则a=______.