设p(x)=x-x²,记[x]为取整函数,即不超过x的最大整数,又设f(x)是二阶连续可微函数,对任意非负整数k,
证明:
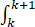 f(x)dx=(f(k+1)+f(k))/2-1/2
f(x)dx=(f(k+1)+f(k))/2-1/2 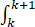 f''(x)p(x-[x]) dx
f''(x)p(x-[x]) dx
设p(x)=x-x²,记[x]为取整函数,即不超过x的最大整数,又设f(x)是二阶连续可微函数,对任意非负整数k,
证明:
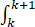 f(x)dx=(f(k+1)+f(k))/2-1/2
f(x)dx=(f(k+1)+f(k))/2-1/2 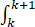 f''(x)p(x-[x]) dx
f''(x)p(x-[x]) dx
暂无答案
设函数f在R上可微,且满足对任意x∈R,有f(x+1)-f(x)=f'(x)以及f' (x)=1,证明:存在常数C,使得f(x)=x+C.
若函数y=f(x)可导,且f'(x0)=1/2,则当∆x→0时,该函数在x=x0处的微分dy是【 】
设函数f:R→R在R/{x0}上有二阶导数,满足:当x∈(-∞,x0)时f' (x)<0<f''(x),而当x∈(x0,+∞)时,f' (x)>0>f''(x),证明:f在x0处不可微.
设f(x)为可导函数且满足(f(1)-f(1+x))/2x=1,则y=f(x)在(1,f(1))处的斜率为【 】
若y=f(x),有f'(x0)=1/2,则当∆x→0时,该函数在x=x0处的微分dy是【 】
求极限(-cotx/e-2x +1/e-xsin²x -1/x²)
设I(x0,x1 )=∬Σ/dydz,其中Σ为抛物面x=y²+z²与平面x=x0,x=x1所围立体表面的内侧,α>0,x1>x0>0,求极限I(x0,x1).
(1)证明:方程(x+1)x+1=exx有唯一正根.(2)若β为(1)中方程的根,计算极限(β+1/n)(β+2/n)⋯(β+n/n).
设α,β是任意非零实数,对正整数n,证明: =其中=α(α-1)⋯(α-k+1)/k!,=1.
设f:[0,1]→(0,+∞)为连续函数,常数a≥1.证明:=a+1.
设f(x)在(-∞,+∞)上可导,且对任意实数x有f(x)=f(x+2k)=f(x+b),其中k为正整数,b为正无理数,用Fourier级数理论证明f(x)为常数.