考研2025年理工数学Ⅰ( )
设函数f(x)在区间[0,+∞)上可导,则【 】
A、当 f(x)存在时,
f(x)存在时, f`(x)存在
f`(x)存在
B、当 f`(x)存在时,
f`(x)存在时, f(x)存在
f(x)存在
C、当
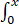 f(t)dt)/x存在时,
f(t)dt)/x存在时, f(x)存在
f(x)存在
D、当 f(x)存在时,
f(x)存在时,
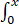 f(t)dt)/x存在
f(t)dt)/x存在
当 f(x)存在时,
f(x)存在时,
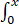 f(t)dt)/x存在
f(t)dt)/x存在
 f(x)存在时,
f(x)存在时,
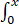 f(t)dt)/x存在
f(t)dt)/x存在解答过程见word版
考研2024年武汉大学( )
设f(x)在(0,+∞)上三次可导,且 f(x)与
f(x)与 f'''(x)均存在,
f'''(x)均存在,
证明: f' (x)=
f' (x)= f'' (x)=
f'' (x)= f'''(x)=0
f'''(x)=0
考研2024年武汉大学( )
设y=arcsinx/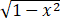 ,求y(2023) (0).
,求y(2023) (0).
考研2023年华中科技大学( )
设p(x)=x-x²,记[x]为取整函数,即不超过x的最大整数,又设f(x)是二阶连续可微函数,对任意非负整数k,
证明:
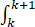 f(x)dx=(f(k+1)+f(k))/2-1/2
f(x)dx=(f(k+1)+f(k))/2-1/2 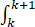 f''(x)p(x-[x]) dx
f''(x)p(x-[x]) dx
考研2024年安徽大学( )
给定方程x²+y + sin(xy)=0.
(1) 说明在点(00)的充分小的邻域内,此方程确定唯一的可导的函数 y=y(x),使得 y(0)= 0,并求出 y=y(x)的导函数表达式.
(2) 判断在点(0,0)的充分小的邻域内,此方程是否确定唯一的函数 x =x(y),使得x(0)=0,说明理由.

