设函数f(x)在区间[0,+∞)上可导,则【 】
A、当 f(x)存在时,
f(x)存在时, f`(x)存在
f`(x)存在
B、当 f`(x)存在时,
f`(x)存在时, f(x)存在
f(x)存在
C、当
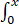 f(t)dt)/x存在时,
f(t)dt)/x存在时, f(x)存在
f(x)存在
D、当 f(x)存在时,
f(x)存在时,
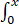 f(t)dt)/x存在
f(t)dt)/x存在
设函数f(x)在区间[0,+∞)上可导,则【 】
A、当 f(x)存在时,
f(x)存在时, f`(x)存在
f`(x)存在
B、当 f`(x)存在时,
f`(x)存在时, f(x)存在
f(x)存在
C、当
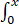 f(t)dt)/x存在时,
f(t)dt)/x存在时, f(x)存在
f(x)存在
D、当 f(x)存在时,
f(x)存在时,
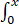 f(t)dt)/x存在
f(t)dt)/x存在
D
【解析】
解答过程见word版
设函数f在R上可微,且满足对任意x∈R,有f(x+1)-f(x)=f'(x)以及f' (x)=1,证明:存在常数C,使得f(x)=x+C.
若y=f(x),有f'(x0)=1/2,则当∆x→0时,该函数在x=x0处的微分dy是【 】
求由方程2y-x=(x-y)ln(x-y)所确定的函数y=y(x)的微分dy.
有一圆柱体底面半径与高随时间变化的速率分别为2cm/s,-3cm/s,当底面半径为10cm,高为5cm时,圆柱体的体积与表面积随时间变化的速率分别为【 】
一卡车沙子通过传送带卸货,假设沙子落到地上堆成一个正圆锥体,且圆锥体的底面半径始终等于圆锥体的高,如果传送带以每分钟3立方米匀速卸沙,问当圆锥达到3米高时,卸了多少时间,此时圆锥高h的增长速度为多少?