设y=arcsinx/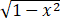
，求y(2023) (0).
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
求极限 (sinx-arctanx)/(tanx-arcsinx)
设二元函数f(x,y)在(x0,y0)的某邻域U内有定义，且在U内存在偏导数.证明：若偏导数fx(x,y)和fy(x,y)都在(x0,y0)可微，则fxy (x0,y0 )=fyx (x0,y0).
设f(x)在(-∞,+∞)上可导，且对任意实数x有f(x)=f(x+2k)=f(x+b)，其中k为正整数，b为正无理数，用Fourier级数理论证明f(x)为常数.
设f:[0,1]→(0,+∞)为连续函数，常数a≥1.证明：=a+1.
设α,β是任意非零实数，对正整数n，证明： =其中=α(α-1)⋯(α-k+1)/k!,=1.
(1)证明：方程(x+1)x+1=exx有唯一正根.(2)若β为(1)中方程的根，计算极限(β+1/n)(β+2/n)⋯(β+n/n).
设I(x0,x1 )=∬Σ/dydz，其中Σ为抛物面x=y²+z²与平面x=x0,x=x1所围立体表面的内侧，α>0,x1>x0>0，求极限I(x0,x1).
已知函数f(x)=x²(ex+1)，则f(5)(1)=___________.
设f(x)在(0,+∞)上三次可导，且f(x)与f'''(x)均存在，证明：f' (x)=f'' (x)=f'''(x)=0
设f(x)=3x3+x2|x|，则使f(n)(0)存在的最高阶n为【 】
已知y=arctanx.(1)证明：2xy'+(1+x2 )y''=0;(2)求y(n).
已知函数f(x)具有任意阶导数，且f' (x)=[f(x)]2，则当n为大于2的正整数时，f(x)的n阶导数f(n) (x)等于【 】
已知函数f(x)=esinx+e-sinx，则f'''(2π)=__________.
设y=y(x)由方程xef(y)=eyln29确定，其中具有二阶导数，f'≠1，则= ____________________.
设函数f(x)在区间(-1,1)内有定义，且f(x)=0，则【 】
设函数y=f(x)由参数方程确定，则x[f(2+2/x)-f(2)]=【 】
设函数f(x)在区间(-1,1)上有定义，且f(x)=0，则【 】
若f(x)=x+lnx,g(x)是f(x)的反函数，则g'' (x)=________.
证明：(f(x0+h)-f(x0-k))/(k+h)存在的充要条件为f在x0处可导.
设函数f在R上可微，且满足对任意x∈R，有f(x+1)-f(x)=f'(x)以及f' (x)=1，证明：存在常数C，使得f(x)=x+C.