已知f(x)在0处n+k(k≥1)次可微,且f(n+i) (0)=0,f(n+k) (0)≠0,i=0,1,⋯,k-1
f(x)=f(0)+f' (0)x+⋯+f(n-1)(0)/(n-1)! x(n-1)+f(n)(θx)/n! xn,求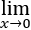 θ.
θ.
已知f(x)在0处n+k(k≥1)次可微,且f(n+i) (0)=0,f(n+k) (0)≠0,i=0,1,⋯,k-1
f(x)=f(0)+f' (0)x+⋯+f(n-1)(0)/(n-1)! x(n-1)+f(n)(θx)/n! xn,求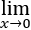 θ.
θ.
使用泰勒展式将f(x)在0处展开:f(x)=f(0)+f' (0)x+⋯+f(n-1)(0)/(n-1)! xn-1+f(n)(0)/n! xn+f(n+k)(0)/(n+k)! xn+k+o(xn+k) ①由已知条件f(x)=f(0)+f' (0)x+⋯+f(n-1)(0)/(n-1)! xn-1+f(n) (θx)/n! xn,...
查看完整答案若f(x),g(x)在[a,b]上可导,∀x∈[a,b],f' (x)≤g'(x),则∀x∈[a,b],f(x)≤g(x).
设函数g(x)在x=0的领域内有定义,g(0)=g'(0)=0,f(x)=,求f'(0).
设f(x)在[a,b]上单调,证明其变上限积分F(x)=f(t)dt在每一x∈(a,b)的单侧导数F+'(x),F_'(x)均存在.
设f(t)=t(1+1/x)2tx ,则f' (t)=__________.
设y=ln(1+ax),其中a是非零常数,则y'=__________,y''=__________.
设f(x)在x=a处可导,则(f(a+x)-f(a-x))/x等于【 】
设f(t)=t(1+1/x)2x,则f' (t)=________________.