计算积分∬SzdS，其中S为曲面x2+z2=2az(a>0)被曲面z=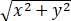
所截的部分.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（2022年同济大学）
答案解析
由对称性，只需计算第一卦限部分.将第一卦限部分在yOz平面作投影Dyz:z=a,z=2a,y=0,2z2=2az+y2.由曲面方程得x=,∴∂x/∂y=0,∂x/∂z=(a-z)/,∴√(1+(∂x/∂y)2+(∂x/∂z)2 )=a/.∴1/4 ∬Sz dS=∬Dyzz a/ dydz=adzz/ dy=√2 az dz令t=，上式=√2 a((2at2+a)2at2)/(1+t2 )3 dt=4√2 a3 t4/(1+t2 )3 dt+2√2 a3 t2/(1+t2 )3 dtt4/(1+t2 )3 dt=[1/(t2+1)-2/(t2+1)2 +1/(t2+1)3 ] dt=1/(t2+1) dt-21/(1+t2 )2 dt+1/(1+t2 )3 dt= arctant|0+∞-21/(1+t2 )2 dt+3/4 1/...
查看完整答案讨论
设D⊂R2是有界单连通闭区域，I(D)=(4-x2-y2)dxdy取得最大值的积分区域记为D1.(1) 求I(D1 )的值.(2) 计算，其中∂D1是D1的正向边界.
设Γ是上半球面x2+y2+z2=R2 (z≥0)上的光滑曲线，起点和终点分别在平面z=0,z=R/2上，曲线的切线与z轴正方向的夹角为常数α∈(0,π/6)，求曲线Γ的长度.
设F=yz(2x+y+z)i+xz(x+2y+z)j+xy(x+y+2z)k.求：F沿螺线r=acost∙i+asint∙j+bt∙k的一段（t:0→π/4）所作的功.
设L为取正向的圆周x2+y2=9，则曲线积分∮L(2xy-2y)dx+(x2 - 4x)dy=________.
计算曲面积分I=∬∑x(8y+1)dydz+2(1-y2 )dxdz-4yzdxdy,其中∑是由曲线(1≤y≤3)绕y轴旋转一周而成的曲面，其法向量与y轴正向的夹角恒大于π/2.
设平面L是下半圆周y=-，则曲线积分∫L(x2+y2)ds=________.
向量场u(x,y,z)=xy2i+ye2j+xln(1+z2)k在点P(1,1,0)处的散度divu=________.
在过点O(0,0)和A(π,0)的曲线族y=asinx(a>0)中，求一条曲线L，使沿该曲线从O到A的积分∫L(1+y3) dx+(2x+y)dy的值最小.
设曲线积分∫L[f(x)-ex]sinydx-f(x)cosydy与路径无关，共中f(x)具有一阶连续导数，且f(0)=0，则f(x)等于【 】
设函数Q(x,y)在xOy平面上具有一阶连续偏导数，曲线积分∫L2xydx+Q(x,y)dy与路径无关，并且对任意t恒有2xydx+Q(x,y)dy=2xydx+Q(x,y)dy，求Q(x,y).
计算曲线积分∮C(z-y)dx+(x-z)dy+(x-y)dz，其中C是曲线从z轴正向往z轴负向看，C的方向是顺时针的.
设L为椭圆x2/4+y2/3=1，其周长记为a，则∮L(2xy+3x2+4y2)ds=__________.
求I=∫L[exsiny-b(x+y)]dx+(excosy-ax)dy，其中a,b为常数，L为从点A(2a,0)沿曲线y=到点O(0,0)的弧.
求∫Cx2ds，其中C为x2+y2+z2=a2 (a>0)与z=的交线.
试问：级数(1+1/2+⋯+1/n)/(n(n+2))是否收敛？若收敛，试求它的和.
设函数项级数ne-nx ,x∈(0,+∞).(1)证明此级数在(0,+∞)上收敛但不一致收敛；(2)求此级数的和函数；(3)给出数项级数n/e3n 的和.