计算积分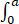
x3 J0 (x)dx
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（2004年春电子科技大学）
答案解析
d(xm Jm (x))/dx=xm Jm-1 (x)KKK(2') x3 J0 (x)dx=x2 xJ0 (x)dx KKK(2' )=x2 d[xJ1 (x)]KKK(2')=a3 J0 (a)-...
查看完整答案讨论
函数f(z)=1/(z-1)(z-2)在圆环区域：(1) 0<|z|<1；(2) 1<|z|<2；(3) 2<|z|<+∞；内是处处解析的。试把f(z)在这些区域内展成洛朗级数。
求将单位圆映射成单位圆且满足条件ω(1/2)=0,ω'(1/2)>0的分式线性映射.
计算：∮cdz/((z2+1)(z2+z+1))，其中c:为|z|<1.
(1)证明初值问题与y(x)=y0+f[t,y(t)]dt等价；(2)若对上式中的积分用辛普生公式，试导出相应的计算格式；并针对初值问题给出计算格式。
对方程组，试问用Jacobi迭代和Gauss-Seidel迭代是否收敛？为什么？
设线性方程组Ax=b的系数矩阵A=。(1)试求能使Jacobi迭代法收敛的a的取值范围；(2)对该方程组写出Jacobi迭代格式（设b=(b1,b2,b3)T已知）。
设平面有界区域D位于第一象限，由曲线x2+y2-xy=1,x2+y2-xy=2与直线y=√3 x,y=0围成，计算∬D1/(3x2+y2 ) dxdy.
设S是单位球面x²+y²+z²=1被锥z>所截部分曲面，定向取球外侧为正向，则对于F=(xy+cosz)i+(-xy-x² )j+(x+2z²)k，曲面积分∬SFdS=________.
设Σ为空间区域{(x,y,z)|x2 + 4y2≤4,0≤z≤2}表面的外侧，则曲面积分∬Σx2dydz + y2dzdx + z2dxdy=______.
设D⊂R2是有界单连通闭区域，I(D)=(4-x2-y2)dxdy取得最大值的积分区域记为D1.(1) 求I(D1 )的值.(2) 计算，其中∂D1是D1的正向边界.
f(x)满足∫f(x)/dx = 1/6·x2 - x + C,L为曲线y=f(x)(4≤x≤9),L的弧长为s,L绕x轴旋转一周所形成的曲面的面积为A，求s和A.
曲线(x2 + y2)2 = x2 - y2 (x≥0,y≥0)与x轴围成的区域为D，求xydxdy.
设D由y=sinπx(0≤x≤1)与x轴转成，则D绕x旋转的旋转体体积为__________.
设Γ是上半球面x2+y2+z2=R2 (z≥0)上的光滑曲线，起点和终点分别在平面z=0,z=R/2上，曲线的切线与z轴正方向的夹角为常数α∈(0,π/6)，求曲线Γ的长度.
计算曲面积分∬S(xdydz+z2dxdy)/(x2+y2+z2 )，其中S是由曲面x2+y2=R2及平面z=R,z=-R(R>0)所围成的立体表面的外侧.
计算曲线积分∮C(z-y)dx+(x-z)dy+(x-y)dz，其中C是曲线从z轴正向往z轴负向看，C的方向是顺时针的.
求I=∫L[exsiny-b(x+y)]dx+(excosy-ax)dy，其中a,b为常数，L为从点A(2a,0)沿曲线y=到点O(0,0)的弧.
求∫Cx2ds，其中C为x2+y2+z2=a2 (a>0)与z=的交线.
计算积分∬SzdS，其中S为曲面x2+z2=2az(a>0)被曲面z=所截的部分.
设L为椭圆x2/4+y2/3=1，其周长记为a，则∮L(2xy+3x2+4y2)ds=__________.
设函数Q(x,y)在xOy平面上具有一阶连续偏导数，曲线积分∫L2xydx+Q(x,y)dy与路径无关，并且对任意t恒有2xydx+Q(x,y)dy=2xydx+Q(x,y)dy，求Q(x,y).
设曲线积分∫L[f(x)-ex]sinydx-f(x)cosydy与路径无关，共中f(x)具有一阶连续导数，且f(0)=0，则f(x)等于【 】
在过点O(0,0)和A(π,0)的曲线族y=asinx(a>0)中，求一条曲线L，使沿该曲线从O到A的积分∫L(1+y3) dx+(2x+y)dy的值最小.