f(x)满足∫f(x)/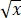
dx = 1/6·x2 - x + C,L为曲线y=f(x)(4≤x≤9),L的弧长为s,L绕x轴旋转一周所形成的曲面的面积为A，求s和A.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（2021年理工数学Ⅱ）
答案解析
f(x)/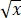 = 1/3·x - 1,f(x) = 1/3·
- 
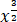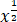x,
曲线的弧长s=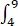
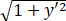dx=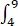
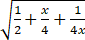dx=22/3.
曲面的侧面积A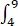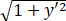=2πdx=2π( - )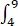
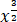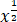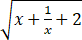dx=425π/9.
讨论
计算 ∬∑x3dydz，其中∑: x2/a2 +y2/b2 +z2/c2 =1,z≥0，取外侧.
已知S={(x,y,z)│x2+4y2+9z2=1,z≤0}取下侧，求∬S(yez+x)dydz+(zex+y)dzdx+(xcosxy+z)dxdy
已知S:(x-5)2+2y2+2(z+1)2=3，方向取外侧，计算∬S((x-5)dydz+ydzdx+zdxdy)/[(x-5)2+y2+z2 ](3/2)
计算曲面积分I=∬Σ(x3+az2)dydz+(y3+ax2)dzdx+(z3+ay2)dxdy，其中Σ为上半球面z=的上侧.
计算积分∬Sx3 dydz+y3 dzdx+z3 dxdy，其中S为球面x2+y2+z2=a2 (a>0)的外侧.
设S是x2+y2+z2=1的外侧，计算∬Sx(x2+1)dydz+y(y2+2)dzdx+z(z2+3)dxdy
设空间有界区域Ω中，柱面x²+y²=1与平面z=0和x+z=1围成，Σ为Ω边界的外侧，计算曲面积分I=∰Σ2xzdydz+xzcosydzdy+3yzsinxdxdy
设平面有界区域D位于第一象限，由曲线x2+y2-xy=1,x2+y2-xy=2与直线y=√3 x,y=0围成，计算∬D1/(3x2+y2 ) dxdy.
设S是单位球面x²+y²+z²=1被锥z>所截部分曲面，定向取球外侧为正向，则对于F=(xy+cosz)i+(-xy-x² )j+(x+2z²)k，曲面积分∬SFdS=________.
设Σ为空间区域{(x,y,z)|x2 + 4y2≤4,0≤z≤2}表面的外侧，则曲面积分∬Σx2dydz + y2dzdx + z2dxdy=______.
确定常数λ，使在右半平面x>0上的向量A(x,y)=2xy(x4+y2 )λ i-x2 (x4+y2 )λ j为某二元函数u(x,y)的梯度，并求u(x,y).
已知曲线L的极坐标方程为r=sin3θ(0≤θ≤π/3)，则L围成有界区域的面积为__________.
求∫C1/(xdx+ydy)，其中C是从(1,0)到(0,2)的光滑曲线（不过原点）.
计算∫Lxdy-ydx，其中L:x2+y2=1，取逆时针方向.
计算积分∬SzdS，其中S为曲面x2+z2=2az(a>0)被曲面z=所截的部分.
求第二类曲线积分∫Ly/(x2+y2)dx-x/(x2+y2)dy，其中L为椭圆x2+1+4y2-4x=0，方向为逆时针.
设D⊂R2是有界单连通闭区域，I(D)=(4-x2-y2)dxdy取得最大值的积分区域记为D1.(1) 求I(D1 )的值.(2) 计算，其中∂D1是D1的正向边界.