设D⊂R2是有界单连通闭区域,I(D)= (4-x2-y2)dxdy取得最大值的积分区域记为D1.
(4-x2-y2)dxdy取得最大值的积分区域记为D1.
(1) 求I(D1 )的值.
(2) 计算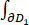
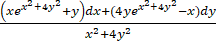 ,其中∂D1是D1的正向边界.
,其中∂D1是D1的正向边界.
设D⊂R2是有界单连通闭区域,I(D)= (4-x2-y2)dxdy取得最大值的积分区域记为D1.
(4-x2-y2)dxdy取得最大值的积分区域记为D1.
(1) 求I(D1 )的值.
(2) 计算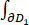
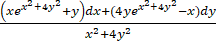 ,其中∂D1是D1的正向边界.
,其中∂D1是D1的正向边界.
(1) 由二重积分的几何意义知:I(D)=(4-x2-y2)dσ,当且仅当4-x2-y2在D上大于0时,I(D)达到最大,故D1:x2+y2≤4且I(D1 )=dθ (4-r2) rdr=8π.(2)...
查看完整答案设un(x) = e-nx + xn+1 (n=1,2,…),求级数un(x)的收敛域和函数.
甲乙两个盒子中各装有2个红球和2个白球,先从甲盒中任取一球,观察颜色后放入乙盒中,再从乙盒中任取一球.令X,Y分别表示从甲盒和乙盒中取到的红球个数,则X与Y的相关系数______.
设A = aij为3阶矩阵,Aij为代数余子式,若A的每行元素之和均为2,且|A| = 3,A11 + A21 + A31 = ______.
设Σ为空间区域{(x,y,z)|x2 + 4y2≤4,0≤z≤2}表面的外侧,则曲面积分∬Σx2dydz + y2dzdx + z2dxdy=______.
计算曲线积分∮C(z-y)dx+(x-z)dy+(x-y)dz,其中C是曲线从z轴正向往z轴负向看,C的方向是顺时针的.
确定常数λ,使在右半平面x>0上的向量A(x,y)=2xy(x4+y2 )λ i-x2 (x4+y2 )λ j为某二元函数u(x,y)的梯度,并求u(x,y).
求I=∫L[exsiny-b(x+y)]dx+(excosy-ax)dy,其中a,b为常数,L为从点A(2a,0)沿曲线y=到点O(0,0)的弧.
已知曲线L的极坐标方程为r=sin3θ(0≤θ≤π/3),则L围成有界区域的面积为__________.
求∫Cx2ds,其中C为x2+y2+z2=a2 (a>0)与z=的交线.
求∫C1/(xdx+ydy),其中C是从(1,0)到(0,2)的光滑曲线(不过原点).
设L为椭圆x2/4+y2/3=1,其周长记为a,则∮L(2xy+3x2+4y2)ds=__________.
设函数Q(x,y)在xOy平面上具有一阶连续偏导数,曲线积分∫L2xydx+Q(x,y)dy与路径无关,并且对任意t恒有2xydx+Q(x,y)dy=2xydx+Q(x,y)dy,求Q(x,y).
在过点O(0,0)和A(π,0)的曲线族y=asinx(a>0)中,求一条曲线L,使沿该曲线从O到A的积分∫L(1+y3) dx+(2x+y)dy的值最小.
设曲线积分∫L[f(x)-ex]sinydx-f(x)cosydy与路径无关,共中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于【 】