关注优题吧，注册平台账号.
设曲面：z=z(x,y)=(y-x2)2+√5/2 x2，柱壁面：9y-9x2+5=0，圆柱体：x2+y2≤1，在三维空间O-XYZ中的“点的集合”分别为G1,G2,G3.
(1)说明“点集”：G=G1∩G2∩G3构成了在三维空间O-XYZ中的有限长度的曲线L.
(2)采用“参数方程”：
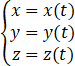，[t∈T；(T为参变数t的“取值集合”)]表示出曲线L.
(3)计算曲线L的“总长度”：L=？
提示：(i)选择参变数t=x,
(ii)考虑柱壁面：y=x2-5/9与圆柱面：x2+y2=1满足相交或满足相切？
[不定积分公式：∫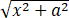
dx=x/2 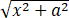+a2/2 ln(x+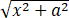)+C可直接引用]
暂无答案
(1)证明初值问题与y(x)=y0+f[t,y(t)]dt等价；(2)若对上式中的积分用辛普生公式，试导出相应的计算格式；并针对初值问题给出计算格式。
从原点向抛物线y=x2+x+1引两条切线，求此二切线与抛物线围成的面积。
试求由曲线y=ex下方，经过坐标原点作y=ex的切线的左侧以及x轴上方构成的图形面积。
求由圆柱面x2+y2=a2,x2+z2=a2 (a>0)所围立体的体积.
设函数f(x)在(-∞,+∞)上有二阶连续导数，证明：f'' (x)≥0的充要条件是：对任意不同的实数a,b,f((a+b)/2)≤1/(b-a)f(x)dx.
设Γ是上半球面x2+y2+z2=R2 (z≥0)上的光滑曲线，起点和终点分别在平面z=0,z=R/2上，曲线的切线与z轴正方向的夹角为常数α∈(0,π/6)，求曲线Γ的长度.
计算：∮cdz/((z2+1)(z2+z+1))，其中c:为|z|<1.
计算sinx/x dxdy，其中D是由直线y=x以及抛物线y=x2围成的区域。
计算∬Dxdxdy，其中D是以O(0,0),A(1,2),B(2,1)为顶点的三角形区域。
设F=yz(2x+y+z)i+xz(x+2y+z)j+xy(x+y+2z)k.求：F沿螺线r=acost∙i+asint∙j+bt∙k的一段（t:0→π/4）所作的功.
计算第二型曲面积分x(x2+1)dydz+y(y2+2)dzdx+z(z2+3)dxdy其中Σ为球面x2+y2+z2=1的外侧.
求I=∫L[exsiny-b(x+y)]dx+(excosy-ax)dy，其中a,b为常数，L为从点A(2a,0)沿曲线y=到点O(0,0)的弧.
求∫Cx2ds，其中C为x2+y2+z2=a2 (a>0)与z=的交线.
计算积分∬SzdS，其中S为曲面x2+z2=2az(a>0)被曲面z=所截的部分.
设D⊂R2是有界单连通闭区域，I(D)=(4-x2-y2)dxdy取得最大值的积分区域记为D1.(1) 求I(D1 )的值.(2) 计算，其中∂D1是D1的正向边界.
计算曲线积分∮C(z-y)dx+(x-z)dy+(x-y)dz，其中C是曲线从z轴正向往z轴负向看，C的方向是顺时针的.
设L为椭圆x2/4+y2/3=1，其周长记为a，则∮L(2xy+3x2+4y2)ds=__________.
设函数Q(x,y)在xOy平面上具有一阶连续偏导数，曲线积分∫L2xydx+Q(x,y)dy与路径无关，并且对任意t恒有2xydx+Q(x,y)dy=2xydx+Q(x,y)dy，求Q(x,y).
设曲线积分∫L[f(x)-ex]sinydx-f(x)cosydy与路径无关，共中f(x)具有一阶连续导数，且f(0)=0，则f(x)等于【 】
在过点O(0,0)和A(π,0)的曲线族y=asinx(a>0)中，求一条曲线L，使沿该曲线从O到A的积分∫L(1+y3) dx+(2x+y)dy的值最小.