已知平面区域D={(x,y)|0≤y≤1/(x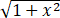 ),x≥1}.
),x≥1}.
(1)求D的面积;
(2)求D绕x轴旋转所成旋转体的体积.
已知平面区域D={(x,y)|0≤y≤1/(x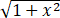 ),x≥1}.
),x≥1}.
(1)求D的面积;
(2)求D绕x轴旋转所成旋转体的体积.
(1)由题设条件可知:S=1/(x√(1+x2 )) dx=x/(x2 √(1+x2 )) dx令t=√(1+x2 ),则上式化为S=t/((t2-1)t) dt=1/2·ln(t-1)/(t+1)...
查看完整答案设f(x)=t|t|dt.求曲线y=f(x)与x轴所围成封闭图形的面积.
点A位于半径为a的圆周内部,且离圆心的距离为b(0≤b<a),从点A向圆周上所有点的切线作垂线,求所有垂足所围成的图形的面积.
(1)证明初值问题与y(x)=y0+f[t,y(t)]dt等价;(2)若对上式中的积分用辛普生公式,试导出相应的计算格式;并针对初值问题给出计算格式。
从原点向抛物线y=x2+x+1引两条切线,求此二切线与抛物线围成的面积。
试求由曲线y=ex下方,经过坐标原点作y=ex的切线的左侧以及x轴上方构成的图形面积。
求由圆柱面x2+y2=a2,x2+z2=a2 (a>0)所围立体的体积.
求由曲面(x2/a2 +y2/b2 +z2/c2 )2=x2/a2 +y2/b2 (a,b,c>0)所围成的空间区域的体积.
求由曲线y=1+sinx与直线y=0,x=0,x=π围成的曲边梯形绕x轴旋转而成的旋转体体积V.
求过曲线y=-x2+1上的一点,使过该点的切线与这条曲线及x,y轴在第一象限围成图形的面积最小,最小面积是多少?
由曲线y=sin3/2x (0≤x≤π)与x轴围成的平面绕x轴旋转而的旋转体的体积为【 】
双纽线(x2+y2)2=x2-y2所围成的区域面积可用定积分表示为【 】
曲线y=cosx(-π/2≤x≤π/2)与x轴所围成的图形,绕x轴旋转一周所成的旋转体的体积为【 】
设抛物线y=ax2+bx+c过原点,当0≤x≤1时,y≥0.又已知抛物线与x轴及直线x=1所围成图形的面积为1/3,试确定a,b,c,使此图形绕x轴旋转一周而成的旋转体的体积V最小.
过点P(1,0)作抛物线y=的切线,该切线与抛物线及x轴围成一个平面图形.求此平面图形绕x轴旋转一周所成旋转体的体积.
设函数f(x)在(-∞,+∞)上有二阶连续导数,证明:f'' (x)≥0的充要条件是:对任意不同的实数a,b,f((a+b)/2)≤1/(b-a)f(x)dx.