关注优题吧，注册平台账号.
设实变量的复值函数u(x,t)满足Cauchy初值问题
iut+uxx=0,-∞<x<+∞,t>0，其中i=√(-1)，
u(x,0)=f(x)为已知函数且满足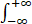
|f(x)|2 dx=1.
(1)求证对任意的t>0，有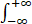|u(x,t)|2 dx≡1.
(2)求证此问题在L2空间中的解是唯一的.
(3)求谐波解u=aei(kx-ωt)(其中，a,k,ω均与自变量x,t无关且k为实数)的色散关系，讨论谐波是否耗散，是否色散，求出谐波的相速度和群速度（以k表达）.
(4)用Fourier变换法求出解的积分表达式.
暂无答案
求解理想不可压缩流体绕圆柱流动的速度势函数u(r,θ)，满足urr+1/r ur+1/r2 uθθ,r>a(半径为a的圆外区域)，ur (a,θ)=0,u=Vrcosθ,V为常数.
求解热传导方程定解问题。ut=uxx-2u 0<x<π,t>0,u(x,0)=sinx,u(0,t)=0,u(π,t)=0.
求解波动方程定解问题。4utt=25uxx -∞<x<+∞,t>0,u(x,0)=sin2x,ut (x,0)=0.
用数学归纳法证明：对于复n维空间Vn上任意多个两两可交换的线性变换所组成的集合S具有公共的特征向量.
设对角矩阵A的特征多项式为 φ(λ)=(λ-λi)ni （诸λi两两互异），求所有和A可交换的矩阵全体所组成的线性空间的维数.
设A=为n×n正定矩阵，证明：|A|≤a11 a22…ann.其中符号|∙|表示行列式.
设A=(aij)n×n为正定矩阵.证明：f(x1,x2,…,xn )=是负定二次型，其中符号|∙|表示行列式.
设A是n×n实对称矩阵，证明：存在一个实数k使得对任意一个实n维向量x都有|x' Ax|≤kx'x，其中x'表示向量x的转置.
由曲线y=sin3/2x (0≤x≤π)与x轴围成的平面绕x轴旋转而的旋转体的体积为【 】
曲线y=cosx(-π/2≤x≤π/2)与x轴所围成的图形，绕x轴旋转一周所成的旋转体的体积为【 】
设抛物线y=ax2+bx+c过原点，当0≤x≤1时，y≥0.又已知抛物线与x轴及直线x=1所围成图形的面积为1/3，试确定a,b,c，使此图形绕x轴旋转一周而成的旋转体的体积V最小.
过点P(1,0)作抛物线y=的切线，该切线与抛物线及x轴围成一个平面图形.求此平面图形绕x轴旋转一周所成旋转体的体积.