求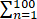 n-1/2 的整数部分.
n-1/2 的整数部分.
问答题(2017年全国大学生决赛)
答案解析
记σ=n-1/2 .由图(1)可知:曲线y=1/√x与x=1,x=100,y=0所围曲边梯形的面积大于它下方的99个长条矩形的面积之和(1/√n∙1) ,于是σ=1+(1/√n∙1) <1+1/√x dx=1+2√x=1+18=19 由图(2)可知:图中99个长条...
查看完整答案讨论
设位于点(0,1)的质点A对质点M的引力大小为k/r2 (k>0,为常数,r为质点A与M之间的距离),质点M沿曲线y=自B(2,0)运动到O(0,0),求在此运动过程中质点A对质点M的引力所做的功.
由曲线y=lnx与两条直线y=e+1-x及y=0所围成的平面图形的面积是______.
求由曲线y=1+sinx与直线y=0,x=0,x=π围成的曲边梯形绕x轴旋转而成的旋转体体积V.
求过曲线y=-x2+1上的一点,使过该点的切线与这条曲线及x,y轴在第一象限围成图形的面积最小,最小面积是多少?
由曲线y=sin3/2x (0≤x≤π)与x轴围成的平面绕x轴旋转而的旋转体的体积为【 】
双纽线(x2+y2)2=x2-y2所围成的区域面积可用定积分表示为【 】
曲线y=cosx(-π/2≤x≤π/2)与x轴所围成的图形,绕x轴旋转一周所成的旋转体的体积为【 】
设抛物线y=ax2+bx+c过原点,当0≤x≤1时,y≥0.又已知抛物线与x轴及直线x=1所围成图形的面积为1/3,试确定a,b,c,使此图形绕x轴旋转一周而成的旋转体的体积V最小.
过点P(1,0)作抛物线y=的切线,该切线与抛物线及x轴围成一个平面图形.求此平面图形绕x轴旋转一周所成旋转体的体积.
设函数f(x)在(-∞,+∞)上有二阶连续导数,证明:f'' (x)≥0的充要条件是:对任意不同的实数a,b,f((a+b)/2)≤1/(b-a)f(x)dx.
(1)证明初值问题与y(x)=y0+f[t,y(t)]dt等价;(2)若对上式中的积分用辛普生公式,试导出相应的计算格式;并针对初值问题给出计算格式。
从原点向抛物线y=x2+x+1引两条切线,求此二切线与抛物线围成的面积。
试求由曲线y=ex下方,经过坐标原点作y=ex的切线的左侧以及x轴上方构成的图形面积。
求由圆柱面x2+y2=a2,x2+z2=a2 (a>0)所围立体的体积.
求由曲面(x2/a2 +y2/b2 +z2/c2 )2=x2/a2 +y2/b2 (a,b,c>0)所围成的空间区域的体积.

