大学数学-考博试题(北京大学 2005年数理方程)

问答题（2005年北京大学）

利用Green函数法求定解问题，

.

答案解析

暂无答案

讨论

大学数学

利用分离变量法求解定解问题

利用积分变换法求解初值问题ut-uxx+u=δ(x)δ(t) -∞<x<+∞,t>0 u(x,0)=0

给定偏微分方程：uxx+4uxy+3uyy=2.(1)化为标准型并求通解；(2)对该方程提定解条件：①u(x,x)=0,ux (x,x)=0或②u(0,y)=0,ux (0,y)=0问哪种定解条件下的定解问题是不适定的？为什么？(3)求出方程满足(2)中适定的定解条件的解。

利用δ函数的性质，计算积分δ(x2+1)sinxdx.

若z=x+iy,f(z)=u(x,y)+iv(x,y)解析，且u-v=(x-y)(x2+4xy+y2)，求f(z).

利用Green函数法求定解问题，

利用积分变换方法求解定解问题，

利用积分变换方法求解定解问题，

给定偏微分方程：uxx+4uxy+3uyy=2.(1)判别方程的类型并求通解；(2)对该方程提定解条件：①u(x,x)=0,ux (x,x)=0或②u(0,y)=0,ux (0,y)=0问哪种定解条件下的定解问题是不适定的？为什么？(3)求出方程满足(2)中适定的定解条件的解。

利用δ函数计算下列积分(x2+1)δ(x2-2x-8)dx.

专业数学

试将sin5θ,cos5θ用sinθ和cosθ表示.

求将单位圆映射成单位圆且满足条件ω(1/2)=0,ω'(1/2)>0的分式线性映射.

设有一根具有绝热的侧表面均匀的细杆，密度为ρ，横截面面积为A，其初始温度为φ(x)，两端满足下列边界条件之一：(1)一端（x=0）绝热，另一端（x=L）有热流密度q进入；(2)一端（x=0）温度为μ1(t)，另一端（x=L）与温度为θ(t)的介质有热交换。试分别写出上述两种热传导过程的定解问题。

电子科技大学复变函数

电子科技大学数理方程

求方程uxx+10uxy+9uyy=0的通解.

写出定解问题的解的表示 ,S:x2+y2+x2=1.

求定解问题对应的贝塞尔方程

设u(x,y)=x2+xy-y2，求出解析函数f(z)=u(x,y)+iv(x,y).

设u(x,y)=ex(xsiny+ycosy)，求出解析函数f(z)=u(x,y)+iv(x,y).

数理方程

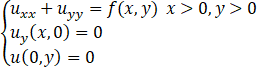设有一根具有绝热的侧表面的均匀细杆，它的初始温度为φ(x)，在一端有热流密度q1进入，另一端与温度为θ(t)的介质有热交换。写出定解问题。

求方程uxx+6uxy-7uyy=0的通解。

求边值问题的固有值和固有函数

电子科技大学数理方程

求解理想不可压缩流体绕圆柱流动的速度势函数u(r,θ)，满足urr+1/r ur+1/r2 uθθ,r>a(半径为a的圆外区域)，ur (a,θ)=0,u=Vrcosθ,V为常数.

求解波动方程定解问题。4utt=25uxx -∞<x<+∞,t>0,u(x,0)=sin2x,ut (x,0)=0.

求解热传导方程定解问题。ut=uxx-2u 0<x<π,t>0,u(x,0)=sinx,u(0,t)=0,u(π,t)=0.

证明微分方程初值问题：的解在α<t<β上存在且惟一，其中a(t),b(t)均在区间α<t<β上连续，α<x_0<β,x_0为任意实数。

设y=φ(x)满足微分不等式dy/dx+a(x)y≤0 其中函数a(x)在x≥0上连续，证明：φ(x)≤φ(0) ,(x≥0).

北京大学齐次微分方程