考研2025年理工数学Ⅰ( )
设Σ是由直线 绕直线 (t为参数)旋转一周得到的曲面,Σ1是Σ介于平面x+y+z=0与x+y+z=1之间部分的外侧,
计算曲面积分∬Σ1xdydz+(y+1)dzdx+(z+2)dxdy.
解答过程见word版
考研2025年理工数学Ⅰ( )
已知有向曲线L是沿抛物线y=1-x²从点A(1,0)到B(-1,0)的一段,则曲线积分∫L(y+cosx)dx+(2x+cosy)dy=______.
4/3-2sin1
解答过程见word版
考研2025年理工数学Ⅰ( )
设函数f(x,y)连续,则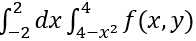 dy=【 】
dy=【 】
A、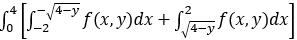 dy
dy
B、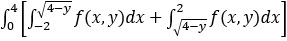 dy
dy
C、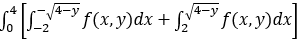 dy
dy
D、2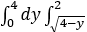 dx
dx
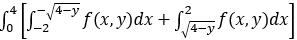 dy
dy解答过程见word版
考研2024年北京邮电大学( )
设有界区域Ω由平面2x+y+2z=2与三个坐标平面围成,Σ为Ω整个表面的外侧,计算曲面积分:
I=∬Σ(x²+1)dydz-2ydzdx+3zdxdy
解答过程见word版
考研2024年北京邮电大学( )
已知L是第一象限中点从点(0,0)沿圆周x²+y²-2x=0到点(2,0),再沿圆周x²+y²=4到点(0,2)的曲线段,计算
I=∫L3x²ydydx+(x³+x-2y)dy
解答过程见word版

