设函数f(x,y)连续,则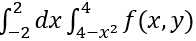 dy=【 】
dy=【 】
A、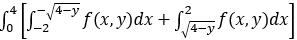 dy
dy
B、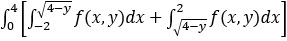 dy
dy
C、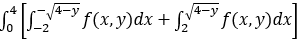 dy
dy
D、2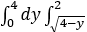 dx
dx
设D是xOy平面上以(1,1),(-1,1)和(-1,-1)为顶点的三角形区域,D1是D在第一象限的部分,则∬D(xy+cosxsiny)dxdy等于【 】
设区域D为x2+y2≤R2,则∬D(x2/a2 +y2/b2 )dxdy=____________.
设函数f(x)在区间[0,1]上连续,并设f(x) dx=A,求dxf(x)f(y)dy.
已知函数f(t)=dxsin(x/y)dy,则f'(π/2)=______.
计算二重积分∬D3x/(x2+xy3 ) dxdy,D:平面曲线xy=1,xy=3,y2=x,y2=3x所围成的有界闭区域.
已知曲线L的极坐标方程为r=sin3θ(0≤θ≤π/3),则L围成有界区域的面积为__________.
计算曲面积分I=∬∑x(8y+1)dydz+2(1-y2 )dxdz-4yzdxdy,其中∑是由曲线(1≤y≤3)绕y轴旋转一周而成的曲面,其法向量与y轴正向的夹角恒大于π/2.
求曲面积分I=∬S yzdzdx+2dxdy,其中S是球面x2+y2+z2=4外侧在z≥0的部分.
设函数f(x)在区间(-1,1)内有定义,且f(x)=0,则【 】
设函数f(x,y)在点(0,0)处可微,f(0,0)=0,n= (∂f/∂x,∂f/∂y,-1)|(0,0),非零向量r与n垂直,则【 】
设A,B,C为三个随机事件,且P(A)=P(B)=P(C)=1/4,P(AB)=0,P(AC)=P(BC)=1/12,则A,B,C中恰有一个事件发生的概率为【 】
计算曲线积分I=∫(4x-y)/(4x²+y² ) dx+(x+y)/(4x²+y² ) dy,其中I是曲线L:x²+y²=2,方向为逆时针方向.
设Σ为曲面z=(1≤x²+y²≤4)的下侧,f(x)是连续函数,计算I=∬Σ(xf(xy)+2x-y)dydz+(yf(xy)+2y+x)dzdx+(zf(xy)+z)dxdy.
计算∫L(x²+y²+z²)ds,其中L:x=acost,y=asint,z=bt,t∈[0,2π].
计算∫Γex(1-cosy)dx-ex(y-siny)dy,其中Γ:y=sinx,x∈[0,π],方向从(π,0)到(0,0).
设P=P(x,y,z),Q=Q(x,y,z)均为连续函数,Σ为曲面z=(x≤0,y≥0)的上侧,则∬ΣPdydz+Qdzdx=【 】
设平面有界区域D位于第一象限,由曲线xy=1/3,xy=3与直线y=1/3 x,y=3x围成,计算∬D(1+x-y)dxdy.
已知平面区域D={(x,y)|√(1-y²)≤x≤1,-1≤y≤1},计算∬Dx/√(x²+y²) dxdy.
已知有向曲线L为球面x²+y²+z²=2x与平面2x-z-1=0交线,从z轴正向往z轴负向看去为逆时针方向,计算曲线积分∫L(6xyz-yz²)dx+2x²zdy+xyzdz.
若D是由(0,0,1),(0,1,1),(1,1,1),(0,0,2),(0,2,2),(2,2,2)组成的R³的一个棱台,则∬D1/(y²+z²) dydz=________.
计算曲面积分∬Sxdydz+ydxdz+zdxdy=________,其中S:x²/a² +y²/b² +z²/c² ≤1,方向向外侧.