已知函数f(x)=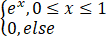
，则
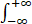dx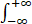f(x)f(y-x)dy=__________.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
已知函数f(x)=esinx+e-sinx，则f'''(2π)=__________.
设二维随机变量(X,Y)的概率分布为X\Y 0 1 2-1 0.1 0.1 b1 a 0.1 0.1若事件{max(X,Y)=2}与事件{min(X,Y)=1}相互独立，则Cov(X,Y)=【 】
设随机变量序列X1,X2,…,Xn,…独立同分布，且X1的概率密度为f(x)=，则当n→∞时，1/n Xi2 依概率收敛于【 】
设随机变量X~N(0,4)，随机变量Y~B(3 ,1/3)，且X与Y不相关，则D(X-3Y+1)=【 】
已知an=-(-1)n/n(n=1,2,…)，则{an}【 】
已知二次型f(x1,x2,x3 )=3x12+4x22+3x32+2x1 x3，(1)求正交变换x=Qy将f(x1,x2,x3)化为标准形；(2)证明minx≠0f(x)/(xT x)=2.
设函数y=f(x)是微分方程2xy'-4y=2lnx-1满足条件y(1)=1/4的解，求曲线y=y(x)(1≤x≤e)的弧长.
计算三重积分∭Ω(x+z)dV，其中Ω是由曲面z=与z=所围成的区域.
求∭Ω(x2+y2+z)dV，其中Ω是由曲线绕z轴旋转一周而成的曲面与平面z=4所围成的立体.
设区域D为x2+y2≤R2，则∬D(x2/a2 +y2/b2 )dxdy=____________.
计算I=∭Ω(x2+y2)dV，其中Ω为平面曲线绕z轴旋转一周形成的曲面与平面z=8所围成的区域.
已知函数f(t)=dxsin(x/y)dy，则f'(π/2)=______.
计算二重积分：∬Dds其中，积分区域D为曲线y(x)=与直线y=0所围成的区域.提示：①首先考察曲线y=y(x)⟹F(x,y)=0为何种曲线，②然后采用“平面极坐标”方法作计算？
计算二重积分∬D3x/(x2+xy3 ) dxdy,D:平面曲线xy=1,xy=3,y2=x,y2=3x所围成的有界闭区域.
设空间区域Ω1:x2+y2+z2≤R2,z≥0,Ω2:x2+y2+z2≤R2,x≥0,y≥0,z≥0，则【 】
设半径为R的球面Σ的球心在定球面x2+y2+z2=a2 (a>0)上，问当R为何值时，球面Σ在定球面内部的那部分的面积最大？
设D是xOy平面上以(1,1),(-1,1)和(-1,-1)为顶点的三角形区域，D1是D在第一象限的部分，则∬D(xy+cosxsiny)dxdy等于【 】
设函数f(x)在区间[0,1]上连续，并设f(x) dx=A,求dxf(x)f(y)dy.
计算∬Ωe(x-y)/(x+y) dΩ，其中Ω:x≥0,y≥0,x+y≤1.
计算 ∬D(√x+y)dxdy，其中D={(x,y)|0≤x≤1,x≤y≤2x}.
求幂级数((-4)n+1)/(4n (2n+1)) x2n 的收敛域及和函数S(x).
已知函数f(x)=，则dxf(x)f(y-x)dy=__________.
已知函数f(x)=，则dxf(x)f(y-x)dy=__________.