求∭Ω(x2+y2+z)dV，其中Ω是由曲线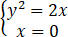
绕z轴旋转一周而成的曲面与平面z=4所围成的立体.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（1991年理工数学Ⅰ）
答案解析
立体在z轴上的投影区域为[0,4]，平行于xOy平面的平面截立体所得的截面x2+y2≤2z(0≤x≤4)，于是∭Ω(x2+y2+z)dV=dzdθ (r2+z)r dr=4πz2 dz=256/3 ...
查看完整答案讨论
设n是曲面2x2+3y2+z2=6在点P(1,1,1)处的指向外侧的法向量，求函数u=/z在点P处沿方向n的方向导数.
设n阶方阵A,B,C满足关系式ABC=E，其中E是n阶单位矩阵，则必有【 】
设D是xOy平面上以(1,1),(-1,1)和(-1,-1)为顶点的三角形区域，D1是D在第一象限的部分，则∬D(xy+cosxsiny)dxdy等于【 】
已知级数(-1)n an=2,a2n-1 =5，则an 等于【 】
若连续函数f(x)满足关系式f(x)=f(t/2)dt+ln2，则f(x)等于【 】
随机地向半圆0<y<(a为常数)内掷一点，点落在半圆内任何区域的概率与该区域的面积与正比，则原点和该点的连续与x轴的夹角小于π/4的概率为__________.
计算二重积分：∬Dds其中，积分区域D为曲线y(x)=与直线y=0所围成的区域.提示：①首先考察曲线y=y(x)⟹F(x,y)=0为何种曲线，②然后采用“平面极坐标”方法作计算？
计算二重积分∬D3x/(x2+xy3 ) dxdy,D:平面曲线xy=1,xy=3,y2=x,y2=3x所围成的有界闭区域.
设空间区域Ω1:x2+y2+z2≤R2,z≥0,Ω2:x2+y2+z2≤R2,x≥0,y≥0,z≥0，则【 】
设半径为R的球面Σ的球心在定球面x2+y2+z2=a2 (a>0)上，问当R为何值时，球面Σ在定球面内部的那部分的面积最大？
计算三重积分∭Ω(x+z)dV，其中Ω是由曲面z=与z=所围成的区域.
已知函数f(t)=dxsin(x/y)dy，则f'(π/2)=______.
计算I=∭Ω(x2+y2)dV，其中Ω为平面曲线绕z轴旋转一周形成的曲面与平面z=8所围成的区域.
已知u是Ω=[0,1]×[0,1]×[0,1]上的正值连续函数，Ip(u)=(∭Ωupdxdydz)1/p证明：Ip(u)=
求(x2+y2+z2 )2=4(x2+y2-z2)所围立体的体积.
已知V是三个坐标平面以及x+y+2z=1,x+y+2z=2围成的封闭区域，求∭V1/(x+y+2z)2 dV
将函数f(x)=arctan(1+x)/(1-x)展开为x的幂级数.
假设λ为n阶可逆矩阵A的一个特征值，证明：(1) 1/λ为A-1的特征值；(2) |A|/λ为A的伴随矩阵A*的特征值.
设随机事件A,B及其和事件A∪B的概率分别是0.4,0.3,0.6，若B ̅表示B的对立事件，那么积事件AB ̅的概率P(AB ̅ )=________.
已知β1,β2是非齐次线性方程组Ax=b的两个不同的解，α1,α2是对应齐次线性方程组Ax=0的基础解系，k1,k2为任意常数，则方程组Ax=b的通解（一般解）必是【 】
设4阶矩阵B=,C=，且矩阵A满足关系式A(E-C-1 B)T CT=E,其中E为4阶单位矩阵，C-1表示 C的逆矩阵，CT表示 C的转置矩阵，将上述关系式化简并求矩阵A.