考研2024年经济数学Ⅲ( )
设f(x,y)是连续函数,则 dx
dx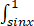 f(x,y)dy=【 】
f(x,y)dy=【 】
A、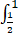 dy
dy 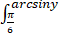 f(x,y)dx
f(x,y)dx
B、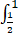 dy
dy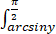 f(x,y)dx
f(x,y)dx
C、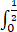 dy
dy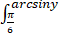 f(x,y)dx
f(x,y)dx
D、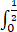 dy
dy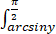 f(x,y)dx
f(x,y)dx
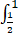 dy
dy 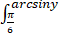 f(x,y)dx
f(x,y)dx考研2024年理工数学Ⅱ( )
设f(x,y)是连续函数,则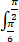 dx
dx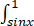 f(x,y)dy=【 】
f(x,y)dy=【 】
A、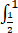 dy
dy f(x,y)dx
f(x,y)dx
B、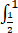 dy
dy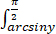 f(x,y)dx
f(x,y)dx
C、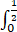 dy
dy f(x,y)dx
f(x,y)dx
D、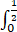 dy
dy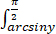 f(x,y)dx
f(x,y)dx
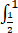 dy
dy f(x,y)dx
f(x,y)dx解答过程见word版
考研2022年吉林大学( )
求三重积分∭Ω(x2+y2)dxdydz,其中积分区域Ω为x2+y2=2z与z=1围成的区域.
原式=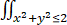 dxdy
dxdy 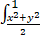 (x2+y2) dz
(x2+y2) dz
=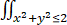 (x2+y2 )(1-(x2+y2)/2) dxdy (1)
(x2+y2 )(1-(x2+y2)/2) dxdy (1)
令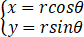 ,J=r,则
,J=r,则
(1)式化为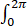 dθ
dθ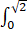 r2 (1-r2/2)∙rdr=2π/3.
r2 (1-r2/2)∙rdr=2π/3.
考研2022年华中科技大学( )
求(x2+y2+z2 )2=4(x2+y2-z2)所围立体的体积.
令x=rcosθsinφ,y=rsinθsinφ,z=rcos,则r=2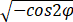 ,φ∈[π/4,π/2]
,φ∈[π/4,π/2]
由于曲面关于三个坐标平面对称,所以
V=8 dθ
dθ 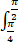 dφ
dφ 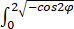 r2 sinφ dr=32π/3
r2 sinφ dr=32π/3 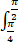 (-cos2φ)3/2 sinφ dφ
(-cos2φ)3/2 sinφ dφ
=32π/3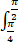 (1-2 cos2φ )3/2 d(-cosφ)
(1-2 cos2φ )3/2 d(-cosφ)
令t=cosφ,上式化为:
V=32π/3 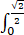 (1-2t2 )3/2 dt
(1-2t2 )3/2 dt
令p2=1-2t2,上式化为:
V=(16√2 π)/3  p4/√(1-p2 ) dp
p4/√(1-p2 ) dp
再令u=p2,上式化为:
V=(8√2 π)/3  u3/2 (1-u)-1/2 du=(8√2 π)/3 B(5/2,1/2)
u3/2 (1-u)-1/2 du=(8√2 π)/3 B(5/2,1/2)
=(8√2 π)/3∙Γ(5/2)Γ(1/2)/Γ(3) =(8√2 π)/3∙(3/4 Γ(1/2)2)/2!=√2 π2
考研2022年武汉大学( )
已知u是Ω=[0,1]×[0,1]×[0,1]上的正值连续函数,Ip(u)=(∭Ωupdxdydz)1/p
证明: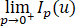 Ip(u)=
Ip(u)=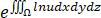
对Ip (u)作恒等变换:
Ip (u)=(∭Ωup dxdydz)1/p=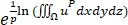
下面考虑1/p ln(∭Ωup dxdydz)的极限.
一般地,对于lnx,有(lnx)'=1/x,(lnx)''=-1/x2 <0,
将lnx在x0处展开:lnx=lnx0+1/x0 (x-x0 )-1/(2!ξ2 ) (x-x0 )2,ξ介于x与x0之间,
故:lnx≤lnx0+1/x0 (x-x0) ①
记x=up,x0=∭Ωup dxdydz,代入①式得:
lnup≤lnx0+1/x0 (up-x0),两边同时积分得:
∭Ωlnup dxdydz≤ln(∭Ωup dxdydz)+1/x0 (∭Ωup dxdydz-∭Ωup dxdydz)=ln(∭Ωup dxdydz)
两边同乘以1/p得:
1/p ∭Ωlnup dxdydz=∭Ωlnu dxdydz=≤1/p ln(∭Ωup dxdydz) ②
另一方面,由于lnx≤x-1,故
1/p ln(∭Ωup dxdydz)≤1/p (∭Ωup dxdydz-1)=1/p (∭Ωup dxdydz-∭Ωdxdydz)=∭Ω(up-1)/p dxdydz ③
由于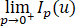 (up-1)/p=lnu,补充定义:├ (up-1)/p┤|p=0=lnu,则(up-1)/p在p=0处右连续,所以:
(up-1)/p=lnu,补充定义:├ (up-1)/p┤|p=0=lnu,则(up-1)/p在p=0处右连续,所以:
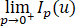 ∭Ω(up-1)/p dxdydz=∭Ω^
∭Ω(up-1)/p dxdydz=∭Ω^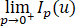 (up-1)/p dxdydz=∭Ωlnu dxdydz
(up-1)/p dxdydz=∭Ωlnu dxdydz
由②③可得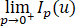 Ip (u)=
Ip (u)=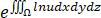 .
.

