已知函数f(x)在x=1处可导且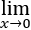
(f(
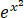)-3f(1+sin2x))/x2 =2，求f'(1).
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（2022年理工数学Ⅱ）
答案解析
由(f()-3f(1+sin2x))/x2 =2可得f()-3f(1+xin2 x)=0，即f(1)=0，又因为(f()-3f(1+sin2x))/x2 =(f()-f(1)-3[f(1+sin2x )-f(1)...
查看完整答案讨论
函数f(x)=(x2-x-2)|x3-x|不可导点的个数是【 】
设f(x)=其中g(x)是有界函数，则f(x)在x=0处【 】
设函数f(x)在(-∞,+∞)内有定义，对任意x都有f(x+1)=2f(x)，且当0≤x≤1时f(x)=x(1-x2)，试判断在x=0处函数f(x)是否可导.
设f(x)可导，F(x)=f(x)(1+|sinx|)，欲使F(x)在x=0可导，则必有【 】
设当x=0时，f(sinx)= f2(sinx)，f'(x)≠0，则f(0)=__________.
已知函数y=f(x)在x=2处连续，且=2求证f(x)在x=2处可导，并求f'(x)=2.
若f(x)在x0的领域内有定义，在x0可导，则f(x)在x0的某领域内连续.
若f(x),g(x)在[a,b]上可导，∀x∈[a,b],f' (x)≤g'(x)，则∀x∈[a,b],f(x)≤g(x).
设f(x)在[a,b]上单调，证明其变上限积分F(x)=f(t)dt在每一x∈(a,b)的单侧导数F+'(x),F_'(x)均存在.
设y=etan(1/x) ∙sin(1/x)，则y'=________________.
设函数g(x)在x=0的领域内有定义，g(0)=g'(0)=0,f(x)=，求f'(0).
设f(t)=t(1+1/x)2tx ，则f' (t)=__________.
已知f'(3)=2，则(f(3-h)-f(3))/2h=________.
设y=ln(1+ax)，其中a是非零常数，则y'=__________，y''=__________.
设f(x)在x=a处可导，则(f(a+x)-f(a-x))/x等于【 】
设f(t)=t(1+1/x)2x，则f' (t)=________________.