函数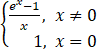 ,在 x=0处【 】
,在 x=0处【 】
A、连续且取得极大值.
B、连续且取得极小值.
C、可导且导数等于零.
D、可导且导数不为零.
函数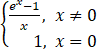 ,在 x=0处【 】
,在 x=0处【 】
A、连续且取得极大值.
B、连续且取得极小值.
C、可导且导数等于零.
D、可导且导数不为零.
D
【解析】
因为f'(0) = 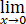
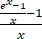 =
= 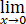
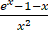 =
= 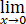
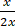 = 1/2,所以 f(x)在x=0可导且导数不等于0.
= 1/2,所以 f(x)在x=0可导且导数不等于0.
已知 fn(x)=求证:(1)对于任何自然数n,方程fn(x)=在区间(0,)中仅有一根;(2)设xn∈(0,)满足fn(xn)=,则.
证明:[x3]+x2=[x2]+x3存在一个非整数解,其中[x]表示不大于x的最大整数.
设函数f(x)在(0,1)上有定义,且函数exf(x)与函数e-f(x)在(0,1)上都是单调递增的,求证:f(x)在(0,1)上连续.
设函数f(x)在x=a可导,且f(a)≠0,则=__________。
设数列{xn}为x1=,x2=,xn+2=(n=1,2,…),求证数列{xn}收敛,并求其极限.
设函数f(x)在(-∞,+∞)内有定义,对任意x都有f(x+1)=2f(x),且当0≤x≤1时f(x)=x(1-x2),试判断在x=0处函数f(x)是否可导.
设f(x)可导,F(x)=f(x)(1+|sinx|),欲使F(x)在x=0可导,则必有【 】
设当x=0时,f(sinx)= f2(sinx),f'(x)≠0,则f(0)=__________.
已知函数y=f(x)在x=2处连续,且=2求证f(x)在x=2处可导,并求f'(x)=2.
设f(x)在x=a的某个领域内有定义,则f(x)在x=a处可导的一个充分条件是【 】
函数f(x)=(x2-x-2)|x3-x|不可导点的个数是【 】
设f(x)=其中g(x)是有界函数,则f(x)在x=0处【 】