设f(x)在x=a的某个领域内有定义,则f(x)在x=a处可导的一个充分条件是【 】
A、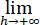 h[f(a+1/h)-f(a)]存在
h[f(a+1/h)-f(a)]存在
B、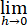 (f(a+2h)-f(a+h))/h存在
(f(a+2h)-f(a+h))/h存在
C、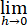 (f(a+h)-f(a-h))/2h存在
(f(a+h)-f(a-h))/2h存在
D、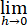 (f(a)-f(a-h))/h存在
(f(a)-f(a-h))/h存在
设f(x)在x=a的某个领域内有定义,则f(x)在x=a处可导的一个充分条件是【 】
A、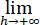 h[f(a+1/h)-f(a)]存在
h[f(a+1/h)-f(a)]存在
B、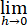 (f(a+2h)-f(a+h))/h存在
(f(a+2h)-f(a+h))/h存在
C、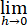 (f(a+h)-f(a-h))/2h存在
(f(a+h)-f(a-h))/2h存在
D、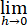 (f(a)-f(a-h))/h存在
(f(a)-f(a-h))/h存在
D
若f(x)在x0的领域内有定义,在x0可导,则f(x)在x0的某领域内连续.
若f(x),g(x)在[a,b]上可导,∀x∈[a,b],f' (x)≤g'(x),则∀x∈[a,b],f(x)≤g(x).
已知f'(3)=2,则(f(3-h)-f(3))/2h=________.
设f(x)可导,F(x)=f(x)(1+|sinx|),则f(x)=0是F(x)在x=0处可导的【 】
设函数f(x)在(-∞,+∞)内有定义,对任意x都有f(x+1)=2f(x),且当0≤x≤1时f(x)=x(1-x2),试判断在x=0处函数f(x)是否可导.
设f(x)可导,F(x)=f(x)(1+|sinx|),欲使F(x)在x=0可导,则必有【 】
设当x=0时,f(sinx)= f2(sinx),f'(x)≠0,则f(0)=__________.
设f(x)在[a,b]上单调,证明其变上限积分F(x)=f(t)dt在每一x∈(a,b)的单侧导数F+'(x),F_'(x)均存在.
一卡车沙子通过传送带卸货,假设沙子落到地上堆成一个正圆锥体,且圆锥体的底面半径始终等于圆锥体的高,如果传送带以每分钟3立方米匀速卸沙,问当圆锥达到3米高时,卸了多少时间,此时圆锥高h的增长速度为多少?
设f(x)为可导函数且满足(f(1)-f(1+x))/2x=1,则y=f(x)在(1,f(1))处的斜率为【 】
由方程xyz+=√2所确定的函数z=z(x,y)在点(1,0,-1)处的全微分dz=____________.
设函数y=y(x)由方程ex+y+cos(xy)=0确定,则dy/dx=__________.
证明:两条心脏线ρ=α(1+cosθ)与ρ=α(1+cosθ)在交点处的切线相互垂直.
设y=y(x)由方程xef(y)=eyln29确定,其中具有二阶导数,f'≠1,则= ____________________.