大学数学-考研试题(理工数学Ⅰ 1991年隐函数及参数方程相关导数)

填空题（1991年理工数学Ⅰ）

设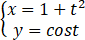，则(d² y)/(dx² )=__________.

答案解析

(sint-tcost)/(4t³)

讨论

大学数学

设二维随机变量(X,Y)在区域D:0<x<1,|y|<x内服从均匀分布，求关于X的边缘概率密度函数及随机变量Z=2X+1的方差D(Z).

质点P沿着以AB为直径的半圆周，从点A(1,2)运动到点B(3,4)的过程中受变力F作用(见图).F的大小等于点P与原点O之间的距离，其方向垂直于线段OP且与y轴正向的夹角小于π/2求变力F对质点P所做的功.

求一个正交变换，化二次型f=x12+4x22+4x32-4x1 x2+4x1 x3-8x2 x3成标准形.

设4阶矩阵B=,C=，且矩阵A满足关系式A(E-C-1 B)T CT=E,其中E为4阶单位矩阵，C-1表示 C的逆矩阵，CT表示 C的转置矩阵，将上述关系式化简并求矩阵A.

设不恒为常数的函数f(x)在闭区间[a,b]上连续，在开区间(a,b)内可导，且f(a)=f(b).证明：在(a,b)内至少存在一点ξ，使得f' (ξ)>0.

求曲面积分I=∬S yzdzdx+2dxdy，其中S是球面x2+y2+z2=4外侧在z≥0的部分.

求幂级数(2n+1) xn 的收敛域，并求其和函数.

求微分方程y''+4y'+4y=e-2x的通解（一般解）.

设z=f(2x-y,ysinx)，其中f(u,v)具有连续的二阶偏导数，求∂2z/∂x∂y.

求ln⁡(1+x)/(2-x)2 dx.

隐函数及参数方程相关导数

证明：两条心脏线ρ=α(1+cosθ)与ρ=α(1+cosθ)在交点处的切线相互垂直.

设函数z=z(x,y)由方程(x+1)z+ylnz-arctan⁡(2xy)=1确定，则 = ______.

设，求dy/dx,(d2 y)/(dx2 ).

已知函数y=y(x)由方程x2+xy+y3=3确定，则y''(1)=__________.

说明理由并证明：在什么条件下，方程F(x1,x2,⋯,xn )=0都能在x0∈Rn附近唯一确定可微函数xj=xj (x1,⋯,xj-1,xj+1,⋯,xn).并在x0附近，求(∂x1)/(∂x2 )(x)∙(∂x2)/(∂x3 )(x)⋯(∂xn-1)/(∂xn )(x)∙(∂xn)/(∂x1 )(x).

设函数y=f(x)由确定，则【】

已知，求 dy/dx|t=0,d2y/dx2|t=0.

设函数z=z(x,y)由ez+xz=2x-y确定，则∂2z/∂x2|(1,1)=________.

已知，求d2y/dx2.

设函数y=y(x)由方程ex+y+cos⁡(xy)=0确定，则dy/dx=__________.

导数与微分

设函数g(x)在x=0的领域内有定义，g(0)=g'(0)=0,f(x)=，求f'(0).

设f(x)在[a,b]上单调，证明其变上限积分F(x)=f(t)dt在每一x∈(a,b)的单侧导数F+'(x),F_'(x)均存在.

设函数f(x)在(-∞,+∞)内有定义，对任意x都有f(x+1)=2f(x)，且当0≤x≤1时f(x)=x(1-x2)，试判断在x=0处函数f(x)是否可导.

设f(x)可导，F(x)=f(x)(1+|sinx|)，欲使F(x)在x=0可导，则必有【】

设当x=0时，f(sinx)= f2(sinx)，f'(x)≠0，则f(0)=__________.

已知函数y=f(x)在x=2处连续，且=2求证f(x)在x=2处可导，并求f'(x)=2.

设y=y(x)由方程xef(y)=eyln29确定，其中具有二阶导数，f'≠1，则= ____________________.

设f(x)=(n=1,2,3,…)，求f(n)(x).

设y=ln(1-x2)，求y(n).

若y=cos , = __________.