设函数y=f(x)由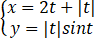 确定,则【 】
确定,则【 】
A、f(x)连续,f'(0)不存在
B、f'(0)存在,f'(x)在x=0处不连续
C、f'(x)连续,f''(0)不存在
D、f''(0)存在,f''(x)在x=0处不连续
设函数y=f(x)由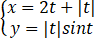 确定,则【 】
确定,则【 】
A、f(x)连续,f'(0)不存在
B、f'(0)存在,f'(x)在x=0处不连续
C、f'(x)连续,f''(0)不存在
D、f''(0)存在,f''(x)在x=0处不连续
C
设F(x)=,其中f(x)在x=0处可导,f' (0)≠0,f(0)=0,则x=0是F(x)的【 】
试问函数f(x,y)=sin[π/(1-x2-y2 )]在区域D:{(x,y)∈R2;x2+y2<1}上是否一致连续?证明你的结论.
证明:f(x)=tx-1 e-t lntdt 在(0,+∞)上连续.
设f(x)在x=0处连续,且对任意的x∈R,有f(x)=f(3x),证明:f(x)是常值函数.
若函数f(x)在[0,1]上连续,f(0)=0,f(1)=1,则对任何自然数n≥1,存在ξ_n∈[0,1],使得f(ξn+1/n)=f(ξn )+1/n.
已知函数f(x)在[a,+∞)上连续,且f(x)存在,证明:(1)函数f(x)有界;(2)存在ξ∈[a,+∞),使得f(ξ)为f(x)在[a,+∞)上的最大值或最小值.
验证函数f(x)=lnx在区间[1,+∞)上一致连续,但在(0,1)上不一致连续.
设函数f(x)在(0,1)上有定义,且函数exf(x)与函数e-f(x)在(0,1)上都是单调递增的,求证:f(x)在(0,1)上连续.
若f(x)在x0的领域内有定义,在x0可导,则f(x)在x0的某领域内连续.
若f(x),g(x)在[a,b]上可导,∀x∈[a,b],f' (x)≤g'(x),则∀x∈[a,b],f(x)≤g(x).
设函数g(x)在x=0的领域内有定义,g(0)=g'(0)=0,f(x)=,求f'(0).
设f(x)在[a,b]上单调,证明其变上限积分F(x)=f(t)dt在每一x∈(a,b)的单侧导数F+'(x),F_'(x)均存在.
设y=etan(1/x) ∙sin(1/x),则y'=________________.
求由方程2y-x=(x-y)ln(x-y)所确定的函数y=y(x)的微分dy.
函数f(x)=(x2-x-2)|x3-x|不可导点的个数是【 】