大学数学-考研试题(华中科技大学 2022年连续函数)

证明题（2022年华中科技大学）

证明：f(x)=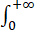t^x-1 e^-t lntdt 在(0,+∞)上连续.

答案解析

记f(x)=tx-1 e-t lntdt +tx-1 e-t lntdt =I1+I2.对于I1,当0<x≤1时，tx-1 e-t lnt= lnt/t1-x =-∞，故t=0为瑕点.对∀[a,b]⊂(0,1],|tx-1 e-t lnt|≤-ta-1 e-t lnt取0<p=1-a/2<1，有-tp ta-1 e-t lnt=-ta/2 lnt=-⁡=⁡2/a ta/2 =0故-ta-1 e-t lntdt 收敛，由魏尔斯特拉斯判别法（M-判别法）知，I1在[a,b]上一致收敛，故在(0,1]内闭一致收敛....

查看完整答案

讨论

连续函数

试问函数f(x,y)=sin⁡[π/(1-x2-y2 )]在区域D:{(x,y)∈R2;x2+y2<1}上是否一致连续？证明你的结论.

设函数f(x)在闭区间[a,b]上连续，(1)证明：f(x)在[a,b]上一定有最大值和最小值（选最小值证明）；(2)进一步，还假设f(x)在[a,b]上处处不为零，试用定义证明函数1/f2(x)在[a,b]上连续.

设f(x)=在(-∞,+∞)内连续，则a=________.

设f(x)=在x=0处连续，则常数a与b应满足的关系是__________.

设F(x)=，其中f(x)在x=0处可导，f' (0)≠0,f(0)=0，则x=0是F(x)的【】

若函数f(x)在[0,1]上连续，f(0)=0,f(1)=1，则对任何自然数n≥1，存在ξ_n∈[0,1]，使得f(ξn+1/n)=f(ξn )+1/n.

已知函数f(x)在[a,+∞)上连续，且f(x)存在，证明：(1)函数f(x)有界；(2)存在ξ∈[a,+∞)，使得f(ξ)为f(x)在[a,+∞)上的最大值或最小值.

验证函数f(x)=lnx在区间[1,+∞)上一致连续，但在(0,1)上不一致连续.

设函数f(x)在(0,1)上有定义，且函数exf(x)与函数e-f(x)在(0,1)上都是单调递增的，求证：f(x)在(0,1)上连续.

反常积分的审敛法

设p为常数，若反常积分lnx/(xp(1-x)1-p) dx收敛，则p的取值范围是【】

讨论sinbx/xλ dx(b≠0)的绝对收敛性和条件收敛性.

求证：J=ln⁡(sinx)dx收敛且J=-π/2 ln2.

证明：广义积分lnx/√x dx收敛.

先说明广义积分dx/(a4+x4 )收敛（a>0是常数），再计算其积分值.

设函数f(x)在[0,+∞)连续、非负，且广义积分f(x)dx收敛，证明：xf(x)dx=0.

证明含参广义积分F(a)=e-axsinxdx在(0,+∞)连续，但非一致收敛.

已知f(x)dx条件收敛，且f+(x)=(|f(x)|+f(x))/2,f-(x)=(|f(x)|-f(x))/2证明：(1) f+(x)dx,f-(x)dx均发散到+∞;(2)当A→+∞时，f+(x) dx与f-(x)dx等价.

求积分I(a)=arctan⁡(ax)/(x(1+x2)) dx,a>0.

判断dx/(ex+1)的敛散性.

函数与极限

当x→0时，α(x),β(x)是非零无穷小量，给出以下四个命题①若α(x)~β(x)，则α2 (x)~β2 (x)②若α2 (x)~β2 (x)，则α(x)~β(x)③若α(x)~β(x)，则α(x)-β(x)=o(α(x))④若α(x)-β(x)=o(α(x))，则α(x)~β(x)其中所有真命题的序号是【】

设函数f(x)在[a,b]上有定义，在(a,b)上连续.下面哪个条件能够判定函数f(x)在[a,b]上有最大值【】

在平面直角坐标系中，椭圆x2+xy+y2=1的长轴方程为__________，位于x轴上半平面内的焦点坐标为__________.

当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【】

考研无穷小与无穷大

设a≠，则ln= .

已知函数f(x)是周期为π的奇函数，且当x∈（0，π/2）时f(x)=sinx-cosx+2，则当x∈（π，π/2）时f(x)=____________________.

函数y=sinx|sinx|（其中|x|≤π/2）的反函数为____________________.

当x→0时，(-1)dt是x7的【】

设a1=1,an=sinan-1 (n≥2)，证明：an≥(n≥2).