已知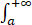 f(x)dx条件收敛,且
f(x)dx条件收敛,且
f+(x)=(|f(x)|+f(x))/2,f-(x)=(|f(x)|-f(x))/2
证明:(1) 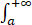 f+(x)dx,
f+(x)dx,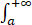 f-(x)dx均发散到+∞;
f-(x)dx均发散到+∞;
(2)当A→+∞时, f+(x) dx与
f+(x) dx与 f-(x)dx等价.
f-(x)dx等价.
已知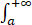 f(x)dx条件收敛,且
f(x)dx条件收敛,且
f+(x)=(|f(x)|+f(x))/2,f-(x)=(|f(x)|-f(x))/2
证明:(1) 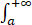 f+(x)dx,
f+(x)dx,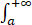 f-(x)dx均发散到+∞;
f-(x)dx均发散到+∞;
(2)当A→+∞时, f+(x) dx与
f+(x) dx与 f-(x)dx等价.
f-(x)dx等价.
(1)由条件知:f(x)=f+ (x)-f- (x),|f(x)|=f+ (x)+f- (x),整理得:|f(x)|=2f+ (x)-(f+ (x)-f- (x))=2f+ (x)-f(x).假如f+ (x) dx收敛,又由已知f(x) dx也收敛,故|f(x)| dx收敛,也已知f(x) dx条件收敛矛盾,所以f+ (x) dx发散到+∞.同样,由已条件可得:...
查看完整答案已知函数f(x)为(A,B)上的连续函数,且有[a,b]⊂(a,b),证明:1/h [f(x+h)-f(x)]dx=f(b)-f(a)
解答如下问题:(1)证明:(-1)n n(n+1)/(n(n+1) x2+2n)关于x∈(-∞,+∞)一致收敛.(2)计算(-1)n n(n+1)/(n(n+1) x2+2n ).
求(x2+y2+z2 )2=4(x2+y2-z2)所围立体的体积.
证明:f(x)=tx-1 e-t lntdt 在(0,+∞)上连续.
已知S:(x-5)2+2y2+2(z+1)2=3,方向取外侧,计算∬S((x-5)dydz+ydzdx+zdxdy)/[(x-5)2+y2+z2 ](3/2)
设p为常数,若反常积分lnx/(xp(1-x)1-p) dx收敛,则p的取值范围是【 】
讨论sinbx/xλ dx(b≠0)的绝对收敛性和条件收敛性.
求证:J=ln(sinx)dx收敛且J=-π/2 ln2.
先说明广义积分dx/(a4+x4 )收敛(a>0是常数),再计算其积分值.
设函数f(x)在[0,+∞)连续、非负,且广义积分f(x)dx收敛,证明:xf(x)dx=0.
证明含参广义积分F(a)=e-axsinxdx在(0,+∞)连续,但非一致收敛.
求积分I(a)=arctan(ax)/(x(1+x2)) dx,a>0.
设[a,+∞)上非负连续函数f可导,且具有连续导函数,若存在r>1,使xf'(x)/f(x)≤-r,证明:反常积分f(x)dx收敛.