解答如下问题:
(1)证明: (-1)n n(n+1)/(n(n+1) x2+2n)关于x∈(-∞,+∞)一致收敛.
(-1)n n(n+1)/(n(n+1) x2+2n)关于x∈(-∞,+∞)一致收敛.
(2)计算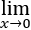
 (-1)n n(n+1)/(n(n+1) x2+2n ).
(-1)n n(n+1)/(n(n+1) x2+2n ).
解答如下问题:
(1)证明: (-1)n n(n+1)/(n(n+1) x2+2n)关于x∈(-∞,+∞)一致收敛.
(-1)n n(n+1)/(n(n+1) x2+2n)关于x∈(-∞,+∞)一致收敛.
(2)计算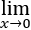
 (-1)n n(n+1)/(n(n+1) x2+2n ).
(-1)n n(n+1)/(n(n+1) x2+2n ).
(1)∵ |(-1)n n(n+1)/(n(n+1) x2+2n )|≤n(n+1)/2n ,而=1/2<1故n(n+1)/2n 收敛.魏尔斯特拉斯判别法(M-判别法)知(-1)n n(n+1)/(n(n+1) x2+2n )关于x∈(-∞,+∞)一致收敛.(2) (-1)n n(n+1)/...
查看完整答案求(x2+y2+z2 )2=4(x2+y2-z2)所围立体的体积.
证明:f(x)=tx-1 e-t lntdt 在(0,+∞)上连续.
已知S:(x-5)2+2y2+2(z+1)2=3,方向取外侧,计算∬S((x-5)dydz+ydzdx+zdxdy)/[(x-5)2+y2+z2 ](3/2)
已知f(x)=,将f(x)展开成正弦级数,并求该级数的和函数.
已知u是Ω=[0,1]×[0,1]×[0,1]上的正值连续函数,Ip(u)=(∭Ωupdxdydz)1/p证明:Ip(u)=
已知{un(x)}是可微函数列,且un(x)在[a,b]上一致有界,证明:若un(x)收敛,则un(x)必定一致收敛.
已知含参变量积分F(x)=sin(xy)/(ln(lny)) dy,证明:(1) F(x)在[δ,+∞)上关于x一致收敛(δ>0)(2) F(x)在(0,+∞)上关于x不一致收敛.
已知f(x)在[a,b]上三次可微,且f(a)=f' (a)=f(b)=0,|f''' (x)|≤M,证明:|f(x) dx|≤M/72 (b-a)4.
设n为正整数,y=yn (x)是微分方程xy' - (n+1)y=0满足条件yn(1)=1/n(n+1)的解.(1) 求yn (x);(2) 求级数yn(x)的收敛域及和函数.
求级数xn/(ln(n!))的收敛半径,并讨论收敛区间端点的收敛情况.
如函数f(x)在[0,+∞)上一致连续,且无穷积分f(x)dx收敛,证明:f(x)=0.
设f(x)在[0,+∞)上非负连续,n是正整数,若f(x)dx存在,则f(x)dx收敛.
设cn(x)在[0,1]上非负连续(n=1,2,…),cn(x)在[0,1]上一致收敛,令Mn=cn(x),问Mn 是否收敛?用(xn(1-x))/lnn验证上面的结论.
将函数f(x)=1/4 ln(1+x)/(1-x)+1/2 arctanx-x展开成x的幂级数.
设f(x)在x=0的某一领域内具有二阶连续导数,且f(x)/x=0,证明级数f(1/n)绝对收敛.
幂级数n/(2n+(-3)n) x2n-1的收敛半径R=________.
设an>0(n=1,2,⋯),且an 收敛,常数λ∈(0,π/2),则级数(-1)n (ntan λ/n) a2n【 】
求幂级数((-4)n+1)/(4n (2n+1)) x2n 的收敛域及和函数S(x).
已知幂级数(-1)nn(n+1) xn .(1)求幂级数的收敛半径、收敛区间以及和函数;(2)计算(-1)nn(n+1)/4n .
设a1,a2,⋯,an是n个实数,都落在区间(-1,1)里.(1)证明 ∏1≤i,j≤n(1+aiaj)/(1-aiaj )≥1(2)找出以上不等式中等号成立的充分必要条件.
函数f(z)=1/(z-1)(z-2)在圆环区域:(1) 0<|z|<1;(2) 1<|z|<2;(3) 2<|z|<+∞;内是处处解析的。试把f(z)在这些区域内展成洛朗级数。