设cn(x)在[0,1]上非负连续(n=1,2,…), cn(x)在[0,1]上一致收敛,令Mn=
cn(x)在[0,1]上一致收敛,令Mn=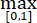 cn(x),问
cn(x),问 Mn 是否收敛?用
Mn 是否收敛?用 (xn(1-x))/lnn验证上面的结论.
(xn(1-x))/lnn验证上面的结论.
问答题(2003年重庆大学)
答案解析
暂无答案
讨论
设f(x)在[a,b]上单调,证明其变上限积分F(x)=f(t)dt在每一x∈(a,b)的单侧导数F+'(x),F_'(x)均存在.
设函数f(x)在[0,+∞)连续,(f(x)-k√x)=0,k>0为常数,证明:f(x)在[0,+∞)上一致连续.
设xn=1+1/√3+1/√5+⋯+1/ - ,证明xn 存在.
计算第二型曲面积分x(x2+1)dydz+y(y2+2)dzdx+z(z2+3)dxdy其中Σ为球面x2+y2+z2=1的外侧.
设x(y),z(y)是由方程组所确定的隐函数,求x'(y),z'(y).
求由圆柱面x2+y2=a2,x2+z2=a2 (a>0)所围立体的体积.
级数n!/nn e-n-x的收敛域为(a,+∞),则a=________.
设函数项级数ne-nx ,x∈(0,+∞).(1)证明此级数在(0,+∞)上收敛但不一致收敛;(2)求此级数的和函数;(3)给出数项级数n/e3n 的和.
已知含参变量积分F(x)=sin(xy)/(ln(lny)) dy,证明:(1) F(x)在[δ,+∞)上关于x一致收敛(δ>0)(2) F(x)在(0,+∞)上关于x不一致收敛.
已知{un(x)}是可微函数列,且un(x)在[a,b]上一致有界,证明:若un(x)收敛,则un(x)必定一致收敛.
解答如下问题:(1)证明:(-1)n n(n+1)/(n(n+1) x2+2n)关于x∈(-∞,+∞)一致收敛.(2)计算(-1)n n(n+1)/(n(n+1) x2+2n ).
设un(x) = e-nx + xn+1 (n=1,2,…),求级数un(x)的收敛域和函数.
设n为正整数,y=yn (x)是微分方程xy' - (n+1)y=0满足条件yn(1)=1/n(n+1)的解.(1) 求yn (x);(2) 求级数yn(x)的收敛域及和函数.

