考虑一个Lebesgue不可测集W⊂[0,1],定义函数
f(x)=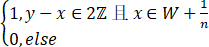
证明: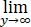 fy(x)=0,但存在一个δ>0,使得对于[0,2]中任意可测子集Eδ,m(Eδ )<δ,当y→∞时,函数列{fy(x)}在[0,2]Eδ上不一致收敛到0.
fy(x)=0,但存在一个δ>0,使得对于[0,2]中任意可测子集Eδ,m(Eδ )<δ,当y→∞时,函数列{fy(x)}在[0,2]Eδ上不一致收敛到0.
考虑一个Lebesgue不可测集W⊂[0,1],定义函数
f(x)=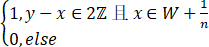
证明: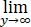 fy(x)=0,但存在一个δ>0,使得对于[0,2]中任意可测子集Eδ,m(Eδ )<δ,当y→∞时,函数列{fy(x)}在[0,2]Eδ上不一致收敛到0.
fy(x)=0,但存在一个δ>0,使得对于[0,2]中任意可测子集Eδ,m(Eδ )<δ,当y→∞时,函数列{fy(x)}在[0,2]Eδ上不一致收敛到0.
暂无答案
分析{(x,y)|x²+y²<1}上的实系统其中的所有奇点,并确定其类型,画出奇点附近的大致图,并与之对应的一次近似系统作比较.
给定x0>0以及[0,+∞)上连续函数f(x),证明:至多具有一个定义于[0,+∞)上的连续函数y(x)满足对任意的x>0,有dy/dx=-y³+f(x),其中y(0)=y0.
设[a,+∞)上非负连续函数f可导,且具有连续导函数,若存在r>1,使xf'(x)/f(x)≤-r,证明:反常积分f(x)dx收敛.
设f在[0,1]上连续,在(0,1)上有二阶连续导数,f(0)=f(1)=1,f'' (x)<8,证明:对任意的x∈[0,1],有f(x)>0.
确定常数a,b,使得极限(axcosx-bsinx)/x³ 存在,并求极限.
设S是单位球面x²+y²+z²=1被锥z>所截部分曲面,定向取球外侧为正向,则对于F=(xy+cosz)i+(-xy-x² )j+(x+2z²)k,曲面积分∬SFdS=________.
设x,t>0,则含参变量积分I(t)=(e-x -e-xt)/x dx=________.
在Oxy平面上给定点O(0,0),A(1,0),动点P(x,y)在直线y=x+1上,则当P(x,y)=________时,∠OPA取到最大.