设[a,+∞)上非负连续函数f可导，且具有连续导函数，若存在r>1，使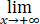
xf'(x)/f(x)≤-r，证明：反常积分
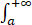f(x)dx收敛.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设f在[0,1]上连续，在(0,1)上有二阶连续导数，f(0)=f(1)=1,f'' (x)<8，证明：对任意的x∈[0,1]，有f(x)>0.
确定常数a,b，使得极限(axcosx-bsinx)/x³ 存在，并求极限.
设S是单位球面x²+y²+z²=1被锥z>所截部分曲面，定向取球外侧为正向，则对于F=(xy+cosz)i+(-xy-x² )j+(x+2z²)k，曲面积分∬SFdS=________.
设x,t>0，则含参变量积分I(t)=(e-x -e-xt)/x dx=________.
在Oxy平面上给定点O(0,0),A(1,0)，动点P(x,y)在直线y=x+1上,则当P(x,y)=________时，∠OPA取到最大.
设矩阵A满足：对任意x1,x2,x3均有A=(1)求A.(2)求可逆矩阵P与对角矩阵A，使得P-1AP=Λ.
设平面有界区域D位于第一象限，由曲线x2+y2-xy=1,x2+y2-xy=2与直线y=√3 x,y=0围成，计算∬D1/(3x2+y2 ) dxdy.