设矩阵A满足:对任意x1,x2,x3均有A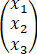 =
=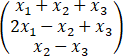
(1)求A.
(2)求可逆矩阵P与对角矩阵A,使得P-1AP=Λ.
设矩阵A满足:对任意x1,x2,x3均有A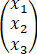 =
=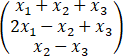
(1)求A.
(2)求可逆矩阵P与对角矩阵A,使得P-1AP=Λ.
(1)因为A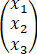 =
=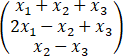 =
=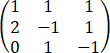
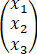 对任意的x1,x2,x3均成立,
对任意的x1,x2,x3均成立,
所以A=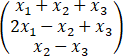 .
.
(2) |λE-A|= =
=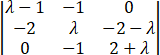 =
=
=(2+λ)(λ2-λ-2)=(λ+2)(λ-2)(λ-1)=0
所以A的特征值为λ1=-2,λ2=2,λ3=-1.
设平面有界区域D位于第一象限,由曲线x2+y2-xy=1,x2+y2-xy=2与直线y=√3 x,y=0围成,计算∬D1/(3x2+y2 ) dxdy.
已知平面区域D={(x,y)|0≤y≤1/(x),x≥1}.(1)求D的面积;(2)求D绕x轴旋转所成旋转体的体积.
已知线性方程组有解,其中a,b为常数.若=4,则=__________.
曲线3x3=y5+2y3在x=1对应点处的法线斜率为__________.
设函数z=z(x,y)由ez+xz=2x-y确定,则∂2z/∂x2|(1,1)=________.
A为4阶方阵,其特征值为-1,1,2,3,A*为A的伴随矩阵,则|A*|=__________。
设A,B是n×n矩阵,φ(λ)为A的特征多项式,证明φ(B)是奇异矩阵的充要条件是A,B有公共的特征值。
设A为n×n复矩阵,证明:存在一个n维向量α,使α,Aα,…,An-1α线性无关的充要条件是A的每个特征向量值恰有一个线性无关的特征向量。
三阶方阵A的特征值为1,-1,2,则A2+4A-1的特征值=________.
设σ为n维线性空间V的一个线性变换,σ2=σ,证明:(1)σ特征值为0,1;(2)设V0,V1分别为0,1对应的特征子空间,则V=V0⊕V1;(3)若σ只有0特征值,则σ为零变换.
假设λ为n阶可逆矩阵A的一个特征值,证明:(1) 1/λ为A-1的特征值;(2) |A|/λ为A的伴随矩阵A*的特征值.
设3阶矩阵A的特征值为λ1=1,λ2=2,λ3=3,对应的特征向量依次为ξ1=,ξ2=,ξ3=,又向量β=.(1)将β用ξ1,ξ2,ξ3线性表出;(2)求An β(n为自然数).
已知α1=,α2=,α3=,记β1=α1,β2=α2 - kβ1,β3=α3 - l1 β1 - l2 β2,若β1,β2,β3 两两正交,则l1,l2依次为【 】
已知矩阵A=与B=相似.(1)求x与y;(2)求一个满足P-1AP=B的可逆矩阵P.
已知ξ=是矩阵A=的一个特征向量.(1)试确定参数a,b及特征向量ξ所对应的特征值;(2)问A能否相似于对角阵?说明理由.
设A为n阶矩阵,|A|≠0,A*为A的伴随矩阵,E为n阶单位矩阵.若A有特征值λ,则(A*)2+E必有特征值____________.
设n阶矩阵A的元素全为1,则A的n个特征值是__________.