设矩阵A=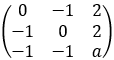，已知1是A的特征多项式的重根.

(1)求a的值；

(2)求所有满足Aα=α+β,A²α=α+2β的非零列向量α,β.

设A,B都为4阶复方阵，则A与B相似当仅当A与B有同的特征多项式，且每个特征值的几何重数(即对应特征子空间的维数)也相同.

设A是n阶非零矩阵，S是使得λA与λ相似的复数λ的集合，证明S是一个有限集. 

假设R是实数域，实向量空间R³中两组向量分别为α₁=(-1,1,0),α₂=(2,-1,2),α₃=(0,1,b)和β₁=(1,0,-1),β₂=(-1,1,1),β₃=(1,1,c).

(1)当b,c取何值时，不存在R³上的线性变换F，满F(α_i )=β_i,i=1,2,3.

(2)当b,c取何值时，至少存在两个R³上的线性变换F，满足F(α_i )=β_i,i=1,2,3.

(3)当b,c取何值时，存在R³上的唯一线性变换F，满足F(α_i )=β_i,i=1,2,3.这样的线性变换是正交变换吗？为什么？

设A，B为2阶矩阵，且AB = BA，则“A有两个不相等的特征值”是“B可对角化”的【 】

A、充分必要条件

B、充分不必要条件

C、必要不充分条件

D、既不充分也不必要条件