大学数学-考研试题(北京理工大学 2022年反常积分的审敛法)

证明题（2022年北京理工大学）

证明：广义积分lnx/√x dx收敛.

答案解析

易知，0为积分瑕点，而lnx/√x<0,x∈(0,1]，所以积分收敛即绝对收敛.

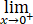x^3/4∙|lnx/√x|=-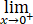lnx/x^-1/4=⁡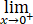4x^1/4=0

所以积分收敛.

讨论

大学数学

证明：级数(2n-1)‼/(n!3n)收敛.

已知：z=x2 F(y/x2)，其中F(u)的一阶偏导数存在，证明：x ∂z/∂x+2y ∂z/∂y=2z.

证明：tanx/x > x/sinx，其中x∈(0,π/2).

已知z=f(u,v)，其中u=2x+y,v=x2，求∂z/∂x,∂z/∂y,∂2/∂x2,∂2z/∂x∂y.

计算∫Lxdy-ydx，其中L:x2+y2=1，取逆时针方向.

计算 ∬D(√x+y)dxdy，其中D={(x,y)|0≤x≤1,x≤y≤2x}.

已知，求d2y/dx2.

求极限( -√n)/

求极限sin4x/(-1)

求证：J=ln⁡(sinx)dx收敛且J=-π/2 ln2.

反常积分的审敛法

设p为常数，若反常积分lnx/(xp(1-x)1-p) dx收敛，则p的取值范围是【】

讨论sinbx/xλ dx(b≠0)的绝对收敛性和条件收敛性.

设函数f(x)在[0,+∞)连续、非负，且广义积分f(x)dx收敛，证明：xf(x)dx=0.

证明含参广义积分F(a)=e-axsinxdx在(0,+∞)连续，但非一致收敛.

已知f(x)dx条件收敛，且f+(x)=(|f(x)|+f(x))/2,f-(x)=(|f(x)|-f(x))/2证明：(1) f+(x)dx,f-(x)dx均发散到+∞;(2)当A→+∞时，f+(x) dx与f-(x)dx等价.

求积分I(a)=arctan⁡(ax)/(x(1+x2)) dx,a>0.

判断dx/(ex+1)的敛散性.

设[a,+∞)上非负连续函数f可导，且具有连续导函数，若存在r>1，使xf'(x)/f(x)≤-r，证明：反常积分f(x)dx收敛.

先说明广义积分dx/(a4+x4 )收敛（a>0是常数），再计算其积分值.

已知二元函数f(x,y)=.(1)求fx(0,y)；(2)证明：fxy(0,0)=-1.

定积分

设f(x)=lnt/(1+t) dt，其中x>0，求f(x)+f(1/x).

设f(x)连续，则d/dx tf(x2-t2)dt等于【】

d/dx sin⁡(x-t)2dt=________.

设I1=x/2(1+cosx) dx,I2=ln⁡(1+x)/(1+cosx) dx,I3=2x/(1+sinx) dx，则【】

积分sinx/(ex+e-x) dx等于【】

设连续函数f(x)满足f(a+b-x)=f(x),∀x∈[a,b]，则积分xf(x)dx等于【】

计算积分xm-1/(1+xn) dx，其中0<m<n.

南京大学定积分的概念与性质

设f∈[0,2π]，证明：f(x)|sinnx|dx=2/πf(x)dx.

设f(a)=0,f(x)在[a,b]上的导数连续，求证：1/(b-a)²·|f(x)|dx≤1/2 maxx∈[a,b] ⁡|f'(x)|,x∈[a,b]