判断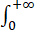 dx/(ex+1)的敛散性.
dx/(ex+1)的敛散性.
问答题(2022年东北大学)
答案解析
∵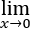 1/(ex+1)=1/2,∴0不是瑕点.
1/(ex+1)=1/2,∴0不是瑕点.
又 x2∙1/(ex+1)=
x2∙1/(ex+1)= 2x/ex =
2x/ex = 2/ex =0,且p=2>1
2/ex =0,且p=2>1
∴由柯西判别法知,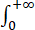 dx/(ex+1)收敛.
dx/(ex+1)收敛.
讨论
求曲面积分∬S(z3-x)dydz-xydzdx-3zdxdy.其中S是由曲面z=4-y2,平面x=0,平面x=3以及xOy平面围成立体的表面,取外侧.
求积分I(a)=arctan(ax)/(x(1+x2)) dx,a>0.
设级数sinnx/(1+nx2)(1)当x取何值时,级数绝对收敛?并说明理由;(2)当x取何值时,级数条件收敛?并说明理由.
设f(x)=(1)求f(x)的傅里叶级数与傅里叶级数的和函数;(2)证明:1/n2 =π2/6.
设f(x)在(0,1)上可导,在[0,1]上连续,且f(1)-f(0)=2e-1-1.证明:存在ξ∈(0,1),使得eξ^2 f' (ξ)+2ξ3=0.
设a,b,c,d皆为常数,cd≠0,说明并给出理由,当a,b,c,d满足什么条件时,f(x)=(ax+b)/(cx+d)无极值.

