关注优题吧，注册平台账号.
设R3上的函数u具有二阶连续偏导数，且不恒为常数，并满足方程∆u+u5=0,∆=∂2/(∂x2 )+∂2/(∂y2 )+∂2/(∂z2 ).令uλ (x,y,z)=λα u(λx,λy,λz),α是某非零常数，使得对任意的λ>0，函数uλ都满足Δuλ+uλ5=0.
(1)求常数α；
(2)若积分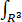
|∇uλ (x,y,z)|2 dxdydz收敛，则对任意的λ>0，以下等式成立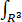：|∇uλ (x,y,z)|2 dxdydz=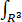|∇u(x,y,z)|2 dxdydz,这里∇=(∂/∂x,∂/∂y,∂/∂z);
(3)假设D是R3中的一个有界光滑曲面∂D围成的区域，且 u|∂D=0，
证明：∫D|u(x,y,z)|6 dxdydz=∫D|∇u(x,y,z)|2 dxdydz.
(1) ∆u+u5=λα+2 ∆u(λx,λy,λz)+λ5α u5 (λx,λy,λz)=0∴α+2=5α解得α=1/2.(2) |∇uλ (x,y,z)|2 dxdydz=|λα+1 ∇u(λx,λy,λz)|2 dxdydz=λ2(α+1)|∇u(λx,λy,λz)|2 dxdydz令λx=ξ,λy=η,λz=ζ上式化为：λ2(α+1) /λ3|∇u(λx,λ...
查看完整答案设u=e-xsin(x/y)，则∂2u)/∂x∂y在点(2,1/π)处的值为________.
设z=1/x·f(xy)+yf(x+y)，求∂2z)/∂x∂y.
若f(x,y)的偏导数fx,fy在(x0,y0)存在，则f(x,y)在(x0,y0)连续.
用变换ξ=x,η=x2+y2化简方程y ∂z/∂x-x ∂z/∂y=0，并求出这个方程的通解z=z(x,y).
二元函数f(x,y)在点(x0,y0)处两个偏导数fx' (x0,y0 ),fy' (x0,y0)存在是f(x,y)在该点连续的【 】
设变换可把方程6 ∂2z/∂x2 +∂2z/∂x∂y-∂2z/∂x∂y=0化简为∂2z/∂u∂v=0，求常数a，其中z=z(x,y)有二阶连续的偏导数.
设f(u)可导，z=xyf(y/x)，若x ∂z/∂x+y ∂z/∂y=xy(lny-lnx)，则【 】
设φ(t),ψ(t)有二阶连续导数，u=φ(y/x)+xψ(y/x)，求：x2 ∂2u/∂x2+2xy ∂2u)/∂x∂y+y2 ∂2u/∂y2.
函数u=ln(x+)在A(1,0,1)处沿A点指向B(3,-2,2)点方向的方向导数为________.
函数f(x,y)=x2+2y2在(0,1)的最大方向导数为______.
设n是曲面2x2+3y2+z2=6在点P(1,1,1)处的指向外侧的法向量，求函数u=/z在点P处沿方向n的方向导数.
函数u=ln(x2+y2+z2)在点M(1,2,-2)处的梯度 gradu|M=__________.
设f(x,y)=，问：f(x,y)在(0,0)处连续吗？方向可导吗？可微吗？
设f(x)在x=0处连续，且对任意的x∈R，有f(x)=f(3x)，证明：f(x)是常值函数.
设a,b,c,d皆为常数，cd≠0，说明并给出理由，当a,b,c,d满足什么条件时，f(x)=(ax+b)/(cx+d)无极值.
设f(x)在(0,1)上可导，在[0,1]上连续，且f(1)-f(0)=2e-1-1.证明：存在ξ∈(0,1)，使得eξ^2 f' (ξ)+2ξ3=0.
计算积分∬Sx3 dydz+y3 dzdx+z3 dxdy，其中S为球面x2+y2+z2=a2 (a>0)的外侧.
计算 ∬∑x3dydz，其中∑: x2/a2 +y2/b2 +z2/c2 =1,z≥0，取外侧.
已知S={(x,y,z)│x2+4y2+9z2=1,z≤0}取下侧，求∬S(yez+x)dydz+(zex+y)dzdx+(xcosxy+z)dxdy
已知S:(x-5)2+2y2+2(z+1)2=3，方向取外侧，计算∬S((x-5)dydz+ydzdx+zdxdy)/[(x-5)2+y2+z2 ](3/2)
计算第二型曲面积分∬S,其中S是下半球面z=-的下侧，a>0是常数.
设Σ为空间区域{(x,y,z)|x2 + 4y2≤4,0≤z≤2}表面的外侧，则曲面积分∬Σx2dydz + y2dzdx + z2dxdy=______.
f(x)满足∫f(x)/dx = 1/6·x2 - x + C,L为曲线y=f(x)(4≤x≤9),L的弧长为s,L绕x轴旋转一周所形成的曲面的面积为A，求s和A.
曲线(x2 + y2)2 = x2 - y2 (x≥0,y≥0)与x轴围成的区域为D，求xydxdy.
设有界区域D是圆x2 + y2 = 1和直线y=x以及x轴在第一象限围成的部分，计算二重积分(x2 - y2)dxdy.