二元函数f(x,y)=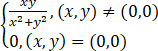
在点(0,0)处【 】
A、连续，偏导数存在
B、连续，偏导数不存在
C、不连续，偏导数存在
D、不连续，偏导数不存在
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设z=1/x·f(xy)+yf(x+y)，求∂2z)/∂x∂y.
若f(x,y)的偏导数fx,fy在(x0,y0)存在，则f(x,y)在(x0,y0)连续.
用变换ξ=x,η=x2+y2化简方程y ∂z/∂x-x ∂z/∂y=0，并求出这个方程的通解z=z(x,y).
二元函数f(x,y)在点(x0,y0)处两个偏导数fx' (x0,y0 ),fy' (x0,y0)存在是f(x,y)在该点连续的【 】
设变换可把方程6 ∂2z/∂x2 +∂2z/∂x∂y-∂2z/∂x∂y=0化简为∂2z/∂u∂v=0，求常数a，其中z=z(x,y)有二阶连续的偏导数.
设φ(t),ψ(t)有二阶连续导数，u=φ(y/x)+xψ(y/x)，求：x2 ∂2u/∂x2+2xy ∂2u)/∂x∂y+y2 ∂2u/∂y2.
设u=e-xsin(x/y)，则∂2u)/∂x∂y在点(2,1/π)处的值为________.
已知z=f(u,v)，其中u=2x+y,v=x2，求∂z/∂x,∂z/∂y,∂2/∂x2,∂2z/∂x∂y.
若f(x,y)在区域D内对x和y都是连续的，则f(x,y)对(x,y)D为二元连续.
设x(y),z(y)是由方程组所确定的隐函数，求x'(y),z'(y).
求函数f(x,y)=1/2(xn+yn)（n是正整数）在条件x+y=a（x≥0,y≥0，常数a>0）下的极值.
设参数方程x=f'(t),y=tf'(t)-f(t)，其中函数f(t)可以求导足够次数，求一阶导数dy/dx和二阶导数d2y/dx2.
设f,g为连续可微函数，u=f(x,xy),v=g(x+xy)，求∂u/∂x∙∂v/∂x
设u=yf(x/y)+xg(y/x)，其中函数f,g具有二阶连续导数，求x ∂2u/∂x2+y ∂2u/∂x∂y .
设z=f(2x-y)+g(x,xy)，其中函数f(t)二阶可导，g(u,v)具有连续的二阶偏导数，求∂2z/∂x∂y.