设f(x)=sinx-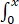
(x-t)f(t)dt，其中f为连续函数，求f(x).
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（1989年理工数学Ⅰ；1989年理工数学Ⅱ）
答案解析
原函数化为f(x)=sinx-xf(t)dt+tf(t)dt, ①两边对x求导得f' (x)=cosx-f(t)dt-xf(x)+xf(x)=cosx-f(t)dt, ②两边再对x求导得f'' (x)+f(x)=-sinx.令x=0，由①②式得f(0)=0,f' (0)=1.于是，原问题转化为求微分方程f'' (x)+f(x)=-sinx满足初始条件f(0)=0,f' (0)=1的特解.方程f'' (x)+f(x)=-s...
查看完整答案讨论
设a1,a2,⋯,an是n个实数，都落在区间(-1,1)里.(1)证明 ∏1≤i,j≤n(1+aiaj)/(1-aiaj )≥1(2)找出以上不等式中等号成立的充分必要条件.
函数f(z)=1/(z-1)(z-2)在圆环区域：(1) 0<|z|<1；(2) 1<|z|<2；(3) 2<|z|<+∞；内是处处解析的。试把f(z)在这些区域内展成洛朗级数。
将函数f(x)=arctan(1+x)/(1-x)展开为x的幂级数.
将函数f(x)=1/4 ln(1+x)/(1-x)+1/2 arctanx-x展开成x的幂级数.
求正的常数a与b，使等式1/(bx-sinx)t2/dt=1成立.
求微分方程y'''+6y''+(9+a2) y'=1的通解，其中常数a>0.
计算曲面积分I=∬∑x(8y+1)dydz+2(1-y2 )dxdz-4yzdxdy,其中∑是由曲线(1≤y≤3)绕y轴旋转一周而成的曲面，其法向量与y轴正向的夹角恒大于π/2.
设在一次试验中，事件A发生的概率为p，现进行n次独立试验，则A至少发生一次的概率为__________；而事件A至多发生一次的概率为__________.
设f(t)=t(1+1/x)2tx ，则f' (t)=__________.
设f(x)是周期为2的周期函数，它在区间(-1,1]上定义为f(x)=，则f(x)的傅里叶级数在x=1处收敛于______.
设4阶矩阵A=(α,γ2,γ3,γ4 ),B=(β,γ2,γ3,γ4)，其中α,β,γ2,γ3,γ4均为四维列向量，且已知行列式|A|=4,|B|=1，则行列式|A+B|=________.
若函数y=f(x)可导，且f'(x0)=1/2，则当∆x→0时，该函数在x=x0处的微分dy是【 】
设y=f(x)是方程y''-2y'+4y=0的一个解，且f(x0)>0,f' (x0)=0，则函数f(x)在点x0处【 】