考虑线性方程组

dx/dt=A(t)x+f(t)  (1)

其中A(t),f(t)以ω为周期，A(t)为n×n的矩阵函数，f(t)为n维向量函数。设x₁ (t),x₂ (t),…,x_n (t)是对应齐次方程组

dx/dt=A(t)x  (2)

的基本解组，满足初始条件：

x₁ (0)=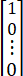,x₂ (0)=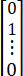,…,x_n (0)=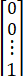 

证明：1.设x=φ(t)是(1)的解，则x=φ(t)是(1)的以ω为周期的周期解的充要条件是φ(0)=φ(ω)。

2.对于任何连续的周期函数f(t),f(t)=f(t+ω)，方程组(1)有惟一的周期解（周期为ω）的充要条件是矩阵X(ω)=[x₁ (ω)…x_n (ω)]没有等于1的特征根。