求固有值问题
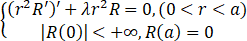
求固有值问题
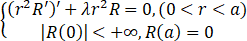
令y=rR(r),则
y'=R+rR',y''=2R'+rR''
ry''+2ry=0
y''+2y=0
λn=(nπ/a)2,Rn (r)=(1/r)sin(nπ/a)r,(n=1,2,Λ)
设函数y=f(x)是微分方程2xy'-4y=2lnx-1满足条件y(1)=1/4的解,求曲线y=y(x)(1≤x≤e)的弧长.
若微分方程y''+ay'+by=0的解在(-∞,+∞)上有界,则【 】
微分方程y''' - y = 0的通解y=_____________________.
设f(x)具有二阶连续导数,f(0)=0,f'(0)=1,且[xy(x+y)-f(x)y]dx+[f'(x)+x2y]dy=0为一阶全微分方程,求f(x)及此全微分方程的通解.
若f(x):(0,π)→R连续,f(x)>0,f(π/2)=1,且对于任意的x∈(0,π)满足dt/(f2(t))=-cosx/(f(x)),求f(x)的表达式.
求微分方程xlnxdy+(y-lnx)dx=0满足条件y|x=e=1的特解.
已知函数y=y(x)在任意点x处的增量Δy=yΔx/(1+x2)+α,且当Δx→0时,α是∆x(∆x→0)的高阶无穷小,y(0)=π,则y(1)等于【 】