给定方程x''+8x'+7x=f(t)，其中f(t)在(-∞,+∞)上连续。如果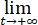
f(t)=0，则上述方程的每一个解当t→+∞时都趋于零。
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
证明：任一可逆的实矩阵A可以表示成A=QB，其中Q为正交矩阵，B是主对角线上元素均为正的三角形矩阵：B=,bii>0,且此表示式是惟一的。
设A=(aij)n×n，且行列式≠0,1≤k≤n.证明存在下三角形矩阵Bn×n，使BA为上三角形矩阵。
设A为m×n且秩为s的矩阵，X为p×m的列满秩矩阵，即r(X)=m，而Y为n×q的行满秩矩阵，即r(Y)=n。证明：r(A)=r(XA)=r(AY)=r(XAY)其中符号r(T)表示矩阵T的秩。
设A为数域P上的一个n级矩阵，如果f(A)=0，则称f(x)以A为根。次数最低首项为1的以A为根的多项式称为A的最小多项式，证明矩阵A的最小多项式是惟一的。
设S1,S3为实对称矩阵，S2为实矩阵，则矩阵S=为正定矩阵的充要条件为矩阵S3与矩阵S1-S2 S3-1 S2'皆为正定矩阵。
设A是n级实对称矩阵，证明rank(A)=n的充要条件是：存在实对称矩阵B使AB+B'A是正定矩阵。
设f(x)具有二阶连续导数，f(0)=0,f'(0)=1，且[xy(x+y)-f(x)y]dx+[f'(x)+x2y]dy=0为一阶全微分方程，求f(x)及此全微分方程的通解.
求微分方程y''+4y'+4y=eax的通解，其中a为实数.
已知函数y=y(x)在任意点x处的增量Δy=yΔx/(1+x2)+α，且当Δx→0时，α是∆x(∆x→0)的高阶无穷小，y(0)=π，则y(1)等于【 】
微分方程y'''-2y''+5y'=0的通解y(x)=__________.
设函数y=f(x)是微分方程2xy'-4y=2lnx-1满足条件y(1)=1/4的解，求曲线y=y(x)(1≤x≤e)的弧长.
微分方程y''' - y = 0的通解y=_____________________.
设a1,a2,⋯,an是n个实数，都落在区间(-1,1)里.(1)证明 ∏1≤i,j≤n(1+aiaj)/(1-aiaj )≥1(2)找出以上不等式中等号成立的充分必要条件.
求解波动方程定解问题。4utt=25uxx -∞<x<+∞,t>0,u(x,0)=sin2x,ut (x,0)=0.
求解热传导方程定解问题。ut=uxx-2u 0<x<π,t>0,u(x,0)=sinx,u(0,t)=0,u(π,t)=0.
求解理想不可压缩流体绕圆柱流动的速度势函数u(r,θ)，满足urr+1/r ur+1/r2 uθθ,r>a(半径为a的圆外区域)，ur (a,θ)=0,u=Vrcosθ,V为常数.
设x1-x2=a1,x2-x3=a2,x3-x4=a3,x4-x5=a4,x5-x1=a5。证明此方程组有解的充分必要条件为ai =0。
证明方程dx/dt=Ax(A为n×n实矩阵)有以ω(ω≠0)为周期的周期解的充要条件是系数矩阵A至少有一个形如i 2πμ/ω的特征根，其中μ为整数。