求正的常数a与b,使等式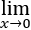 1/(bx-sinx)
1/(bx-sinx)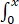 t2/
t2/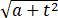 dt=1成立.
dt=1成立.
计算题(1987年理工数学Ⅰ)
答案解析
根据洛必达法则,有1/(bx-sinx) t^2/dt==1,又=0,(b-cosx)=b-1,从而b=1,于是1/(bx-sinx) t^2/dt==∙=1/√a =2/√a=1,解得a=4...
查看完整答案讨论
设A为n阶方阵,且A的行列式|A|=a≠0,而A*是A的伴随矩阵,则|A* |等于【 】
设(f(x)-f(a))/(x-a)2=-1,则在x=a处【 】
若f(x)为已知连续函数,I=tf(tx)dx,其中t>0,s>0,则I的值【 】
已知三维向量空间的基底为α1=(1,1,0)T,α2=(1,0,1)T,α3=(0,1,1)T,则向量β=(2,0,0)T在此基底下的坐标是____________.
设L为取正向的圆周x2+y2=9,则曲线积分∮L(2xy-2y)dx+(x2 - 4x)dy=________.
与两直线及(x+1)/1=(y+2)/2=(z-1)/1都平行且过原点的平面方程为______________.
已知A=(1) 求正交矩阵P,使得PTAP为对角矩阵;(2) 求正定矩阵C,使得C2 = (a+3)E-A.
设f(x)在[0,1]上具有二阶导数,且满足条件|f(x)|≤a,|f''(x)|≤b,其中a,b都是非负常数,c是(0,1)内任意一点,证明:|f'(c)|≤2a+b/2.
设直线l:在平面π上,且平面π与曲面z=x2+y2相切于点(1,-2,5),求a,b的值.
设B是秩为2的5×4矩阵,α1=(1,1,2,3)T,α2=(-1,1,4,-1)T,α3=(5,-1,-8,9)T是齐次线性方程组Bx=0的解向量,求Bx=0的解空间的一个标准正交基.
函数f(x)=(x2-x-2)|x3-x|不可导点的个数是【 】
已知函数y=y(x)在任意点x处的增量Δy=yΔx/(1+x2)+α,且当Δx→0时,α是∆x(∆x→0)的高阶无穷小,y(0)=π,则y(1)等于【 】
求函数f(x)=x2/(1+x2 )的极值与拐点,并求拐点处的切线方程.
当x→0时,1-cosxcos2xcos3x对于无穷小x的阶数等于 __________.
不查表,求方程x2sin=2x-1977的近似解,精确到0.001.
设x>0时,f(x)=,求证:x→0+时,f(x)=e+Ax+Bx2+o(x2),并求A,B之值.
设函数f(x)=ax-blnx(a>0)有两个零点,则b/a的取值范围是【 】
设函数f(x)=secx在x=0处的2次泰勒多项式为1+ax+bx2,则【 】
设x0,x1,…,xn为n+1个互异的插值节点,li (x)(i=0,1,…,n)为拉格朗日基本插值多项式(也称为插值基本函数)。证明:(1) li (x)≡1;(2) li (x)xik≡xk.

