去年，张师傅因为多旋圈面爆红，今年他来到了达摩院给扫地僧做面。某天，软件工程师小李跟张师傅吐槽工作。小李主要硏究和设计算法用于调节各种产品的参数。这样的参数一般可以通过极小化Rⁿ上的某个损失函数f求得。在小李最近的一个项目中，这个损失函数是另外一个课题组提供的；出于安全考虑和技术原因，该课题组难以向小李给出此函数的内部细节，而只能提供一个接口用于计算任意x∈Rⁿ处的函数值f(x)。所以，小李必须仅基于函数值来极小化f。而且，每次计算f的值都消耗不小的计算资源。好在该问题的维度n不是很高(10左右)。另外，提供函数的同事还告知小李不妨先假设f是光滑的。

这个问题让张师傅想起了自己收藏的一台古董收音机。要在这台收音机上收听一个节目，你需要小心地来回拧一个调频旋钮，同时注意收音效果，直到达到最佳。在这过程中，没有人确切地知道旋钮的角度和收音效果之间的定量关系是什么。张师傅和小李意识到，极小化f不过就是调节一台有多个旋钮的机器：想象x的每一个分量由一个旋钮控制，而f(x)表示这台机器的某种性能，只要我们来回调整每个旋钮，同时监视f的值，应该就有希望找到最佳的x。受此启发，两人一起提出了极小化f的一个迭代算法，并命名为“自动前后调整算法”( Automated Forward/Backward Tuning，AFBT，算法1)。在第k次迭代中，AFBT通过前后调整x_k的单个分量得2n个点{x_k±t_k eⁱ:i=1,…,n}，其中t_k为步长；然后，令y_k为这些点中函数值最小的一个，并检査y_k是否使f充分减小；若是，取x_k+1=y_k，并将步长增倍；否则，令x_k+1=x_k并将步长减半。在算法1中，eⁱ表示Rⁿ中的第i个坐标向量，它的第i个分量为1，其余皆为0； I(∙) 为指示函数——若f(x_k )-f(y_k)至少为t_k之平方，则I[f(x_k )-f(y_k )≥t_k²]取值为1，否则为0。

1自动前后调整算法(AFBT)

输入x₀∈Rⁿ,t₀>0。对k=0,1,2,…，执行以下循环。

1：y_k≔argmin{f(y):y=x_k±t_k eⁱ,i=1,…,n}   #计算损失函数。

2：s_k≔I[f(x_k )-f(y_k )≥t_k²]    #是否充分下降？是：s_k=1；否：s_k=0。

3：x_k+1≔(1-s_k ) x_k+s_k y_k    #更新迭代点。

4：t_k+1≔2^{(2s_k-1 )} t_k    #更新步长。s_k=1：步长增倍；s_k=0：步长减半。

现在，我们对损失函数f:Rⁿ→R作出如下假设。

假设1. f为凸函数，即对任何x,y∈Rⁿ与α∈[0,1]都有

f((1-α)x+αy)≤(1-α)f(x)+αf(y).

假设2. f在Rⁿ上可微且∇f在Rⁿ上 L-Lipschitz连续。

假设3. f的水平集有界，即对任意λ∈R，集合{x∈Rⁿ:f(x)≤λ}皆有界。

基于假设1与假设2，可以证明

〈∇f(x),y-x〉≤f(y)-f(x)≤〈∇f(x),y-x〉+L/2 ‖x-y‖²

对任何x,y∈Rⁿ成立；假设1与假设3则保证f在Rⁿ上取到有限的最小值f^*。凸函数的更多性质可参考任何一本凸分析教科书。

证明题(20分) 在假设1-3下，对于AFBT，证明

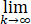f(x_k)=f^*.