设曲线y=y(x)(x>0)经过点(1,2),该曲线上任一点P(x,y)到y轴的距离等于该点处的切线在y轴上的截距.
(Ⅰ)求y(x);
(Ⅱ)求函数f(x)=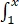 y(t)dt在(0,+∞)上的最大值.
y(t)dt在(0,+∞)上的最大值.
设曲线y=y(x)(x>0)经过点(1,2),该曲线上任一点P(x,y)到y轴的距离等于该点处的切线在y轴上的截距.
(Ⅰ)求y(x);
(Ⅱ)求函数f(x)=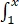 y(t)dt在(0,+∞)上的最大值.
y(t)dt在(0,+∞)上的最大值.
(Ⅰ)设点(x,y)处的切线方程为Y-y=y'(X-x),故y轴的截距为y-y'x,则x=y-y'x,解得y=x(C-lnx),其中C为任意常数.由y(1)=C=2,故y(x)=x(2-lnx).(Ⅱ)由(Ⅰ)知,f(x)=t(2-lnt)dt,故f...
查看完整答案设随机变量X与Y相互独立,且X~B(1,1/3),Y~(2,1/2),则P{X=Y}=______.
已知向量α1=,α2=,α3=,β=,γ=k1 α1+k2 α2+k3 α3,若γTαi=βTαi (i=1,2,3),则k12+k22+k32=______.
设连续函数f(x)满足f(x+2)-f(x)=x,f(x)dx=0,则f(x)dx=______.
设f(x)为周期为2的周期函数,且f(x)=1-x,x∈[0,1],若f(x)=a0/2+ancosnπx,则a2n =________.
曲面z=x+2y+ln(1+x2+y2)在(0,0,0)处的切平面方程为__________.
当x→0时,函数f(x)=ax+bx2+ln(1+x)与g(x)=ex^2 -cosx是等价无穷小,则ab=______.
设X1,X2为来自总体N(μ,σ2)的简单随机样本,其中σ(σ>0)是未知参数.若σ ̂=a|X1-X2 |为σ的无偏估计,则a=【 】
已知f(x)在x=0的某个领域内连续,且f(0)=0,f(x)/(1-cosx)=2,则在点x=0处f(x)【 】
若g(x)在x=c处二阶导数存在,且g' (c)=0,g'' (c)<0,则g(c)为g(x)的一个极大值.
将长为a的铁丝切成两段,一段围成正方形,另一段围成圆,问这两段铁丝长各为多少时,正方形与圆的面积之和为最小?
设两函数f(x)及g(x)都在x=a处取得极大值,则函数F(x)=f(x)g(x)在x=a处【 】
在椭圆x2/a2 +y2/b2 =1的第一象限上求一点P,使该点处的切线、椭圆及两坐标轴所围成图形面积为最小(其中a>0,b>0).
试求椭圆x2/4+y2=1上一点,使其到直线3x+4y-12=0,3x-4y+12=0和y+3=0的距离平方和最小.
设a,b,c,d皆为常数,cd≠0,说明并给出理由,当a,b,c,d满足什么条件时,f(x)=(ax+b)/(cx+d)无极值.