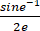大学数学-考研试题(高等数学三 2021年函数的微分)

填空题（2021年经济数学Ⅲ）

若y=cos , = __________.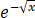

答案解析

讨论

大学数学

总体X的概率分布为P{X=1}=(1-θ)/2,P{X=1}=P{X=3}=(1+θ)/4，利用来自总体X的样本观察值1,3,2,2,1,3,1,2可得θ的最大似然估计值为【】

设A=(α1,α2,α3,α4)为4阶正交矩阵，若矩阵A = ,β = ,k表示任意常数，则线性方程组Ax=β的通解为x=【】

设矩阵A=仅有两个不同的特征值.若A相似于对角矩阵，求a,b的值，并求可逆矩阵P，使P-1AP为对角矩阵.

曲线(x2 + y2)2 = x2 - y2 (x≥0,y≥0)与x轴围成的区域为D，求xydxdy.

设函数y=y(x)的微分方程xy' - 6y = -6，满足y()=10,(1) 求y(x);(2) P为曲线y=y(x)上的一点，曲线y=y(x)在点P的法线在y轴上的截距为Iy，为使Iy最小，求P的坐标.

f(x)满足∫f(x)/dx = 1/6·x2 - x + C,L为曲线y=f(x)(4≤x≤9),L的弧长为s,L绕x轴旋转一周所形成的曲面的面积为A，求s和A.

已知f(x)=，求f(x)的凹凸性及渐近线.

多项式f(x)=中x3项的系数为______.

微分方程y''' - y = 0的通解y=_____________________.

已知函数f(t)=dxsin(x/y)dy，则f'(π/2)=______.

函数的微分

有一圆柱体底面半径与高随时间变化的速率分别为2cm/s，-3cm/s，当底面半径为10cm，高为5cm时，圆柱体的体积与表面积随时间变化的速率分别为【】

若y=f(x)，有f'(x0)=1/2，则当∆x→0时，该函数在x=x0处的微分dy是【】

设tany=x+y，则dy=__________.

已知，求dy/dx,d2y/dx2

求由方程2y-x=(x-y)ln⁡(x-y)所确定的函数y=y(x)的微分dy.

如果y=(x+t)dt，则 dy/dx|x=0等于【】

设函数f:R→R在R/{x0}上有二阶导数，满足：当x∈(-∞,x0)时f' (x)<0<f''(x)，而当x∈(x0,+∞)时，f' (x)>0>f''(x)，证明：f在x0处不可微.

若函数y=f(x)可导，且f'(x0)=1/2，则当∆x→0时，该函数在x=x0处的微分dy是【】

已知z=arctan (x+y)/(x-y)，求dz.

设f(x)为可导函数且满足(f(1)-f(1+x))/2x=1，则y=f(x)在(1,f(1))处的斜率为【】

导数与微分

设函数z=z(x,y)由方程(x+1)z+ylnz-arctan⁡(2xy)=1确定，则 = ______.

证明：两条心脏线ρ=α(1+cosθ)与ρ=α(1+cosθ)在交点处的切线相互垂直.

设y=y(x)由方程xef(y)=eyln29确定，其中具有二阶导数，f'≠1，则= ____________________.

设f(x)=(n=1,2,3,…)，求f(n)(x).

设y=ln(1-x2)，求y(n).

设函数y=y(x)由参数方程确定，则=_______.

已知函数y=y(x)由方程x2+xy+y3=3确定，则y''(1)=__________.

已知y=arctanx.(1)证明：2xy'+(1+x2 )y''=0;(2)求y(n).

设f(x)=3x3+x2|x|，则使f(n)(0)存在的最高阶n为【】

说明理由并证明：在什么条件下，方程F(x1,x2,⋯,xn )=0都能在x0∈Rn附近唯一确定可微函数xj=xj (x1,⋯,xj-1,xj+1,⋯,xn).并在x0附近，求(∂x1)/(∂x2 )(x)∙(∂x2)/(∂x3 )(x)⋯(∂xn-1)/(∂xn )(x)∙(∂xn)/(∂x1 )(x).