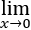大学数学-考研试题(中国科学院 2022年洛必达法则)

计算题（2022年中国科学院）

(ln⁡(1+x)-x)/x²

答案解析

应用洛必达法则，对分子、分母同时求导有：(ln⁡(1+x)-x)/x2 =(1/(1+x)-1)/2x,再次使用洛必达法则：(1/(1+x)-1)/2x=(-1)/(2(1+x)2 )=-1/2.∴原...

查看完整答案

讨论

泰勒公式

设f(x)在[0,1]上具有二阶导数，且满足条件|f(x)|≤a,|f''(x)|≤b，其中a,b都是非负常数，c是(0,1)内任意一点，证明：|f'(c)|≤2a+b/2.

设x>0时，f(x)=，求证：x→0+时，f(x)=e+Ax+Bx2+o(x2)，并求A,B之值.

设函数f(x)=sinx/(1+x2)在x=0处的3次泰勒多项式为ax+bx2+cx3，则【】

设函数f(x)在区间[0,1]上连续，则f(x)dx=【】

当x→0时，x-sinxcosxcos2x与cx4为等价无穷小，则c=__________，k=__________.

当x→0时，1-cosxcos2xcos3x对于无穷小x的阶数等于 __________.

设函数f(x)=secx在x=0处的2次泰勒多项式为1+ax+bx2，则【】

已知f(x)在[a,b]上二阶可导，且f''(x)≤0，证明：f(x)dx≤(b-a)f((a+b)/2).

求∫Cx2ds，其中C为x2+y2+z2=a2 (a>0)与z=的交线.

求∫C1/(xdx+ydy)，其中C是从(1,0)到(0,2)的光滑曲线（不过原点）.

洛必达法则

求正的常数a与b，使等式1/(bx-sinx)t2/dt=1成立.

已知 =c（c≠0），求k和c.

试求椭圆x2/4+y2=1上一点，使其到直线3x+4y-12=0,3x-4y+12=0和y+3=0的距离平方和最小.

设u∈C2 (R3)且∆u(x)=((∂2 u)/(∂x12 )+(∂2 u)/(∂x22 )+(∂2 u)/(∂x32 ))(x)=λu(x),λ为正常数，已知存在C>0，使得|x|≥C时，u≡0，求证：u(x)≡0,∀x∈R3.

设f∈[0,2π]，证明：f(x)|sinnx|dx=2/πf(x)dx.

求证：(-1)n-1x2/(1+x2 )n 在R上一致收敛.

求证：x2/(1+x2 )n 收敛，但在R上不一致收敛.

(1+22√2+32∛3+⋯+n2)/n3

讨论sinbx/xλ dx(b≠0)的绝对收敛性和条件收敛性.

中值定理与导数的应用

设函数f(x)在(0,+∞)上连续可导，f(x)存在，f(x)的图形在(0,+∞)是上凸的，求证：f′(x)=0.

不查表，求方程x2sin=2x-1977的近似解，精确到0.001.

设函数f(x)=ax-blnx(a>0)有两个零点，则b/a的取值范围是【】

已知f(x)=，求f(x)的凹凸性及渐近线.

设x0,x1,…,xn为n+1个互异的插值节点，li (x)(i=0,1,…,n)为拉格朗日基本插值多项式（也称为插值基本函数）。证明：(1) li (x)≡1;(2) li (x)xik≡xk.

两实变量x与y之间存在“变化关系”，且“变化关系”满足方程：e-1/3 x+2y+(e10/3 - 1)∙e-1/3 x+y - ex^3+2x^2-2x =0.(1)确定出y关于x的单值、连续的函数关系式(解析式)：y=f(x)=?及其函数f(x)的定义域{x}=?提示：求解函数方程以及求解其后问题时，令：e10/3-1=2a，可便于计算分析处理.(2)求出函数y=f(x)的一阶导数：dy/dx=f'(x)=?及其可导区域{x}=?(3)绘出函数y=f(x)的图像草图.提示:(i)首先寻找出函数f(x)的三个“零点”：xk=? [其中，f(xk )=0,(k=1,2,3)],以及一阶导数函数f'(x)的两个“零点”xl[其中，f' (xl' )=0,(l=1,2)](ii)然后，考察函数f(x)的渐近性质： f(x)|x→±∞→?(iii)最后，利用(i)和(ii)的结果，便可绘制出函数y=f(x)的图像草图.[注意:“零点”方程f(xk )=0最终可化为关于xk的三次方程，可采用(分组分解法)因式分解后再作求解]

已知三个关于自变量x的函数：y=f(x),z=g(x),t=h(x)，其“函数关系”由如下“隐函数方程组”确定出： (1)确定出y,z,t关于x的单值、连续的函数关系式（解析式）：y=f(x)=?,z=g(x)=?,t=h(x)=?及其各函数的定义域{x}=?提示：求解函数方程以及求解其后问题时，令e10/3 - 1=2a，可便于计算分析处理。(2)求出函数y=f(x)的一阶导数：dy/dx=f' (x)=?及其可导区域{x}=?(3)给出函数y=f(x)的图像草图.提示：①首先，寻找出函数f(x)的三个“零点”：xk=?[其中，f(xk )=0;(k=1,2,3)],以及一阶导数函数f'(x)的两个“零点”：xl'=?[其中，f' (xl' )=0;(l=1,2)].②然后，考察函数f(x)的渐近性质.③最后，利用①②的结果，便可绘制出函数f(x)的图像草图[注意：“零点”方程f(xk )=0最终可化为关于xk的三次方程，可采用（分组分解法）因式分解后再作求解].

求函数f(x)=x2/(1+x2 )的极值与拐点，并求拐点处的切线方程.

设函数f(x)在开区间(a,b)内存在二阶导数f''(x)，且在(a,b)内f''(x)>0，证明：对于任意两点x1,x2∈(a,b)，恒有f((x1+x2)/2)≤(f(x1)+f(x2))/2.

曲线y=(t-1)(t-2)dt在点(0,0)处的切线方程是____________.