已知三个关于自变量x的函数:y=f(x),z=g(x),t=h(x),其“函数关系”由如下“隐函数方程组”确定出:
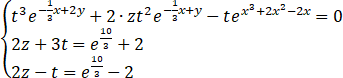
(1)确定出y,z,t关于x的单值、连续的函数关系式(解析式):y=f(x)=?,z=g(x)=?,t=h(x)=?及其各函数的定义域{x}=?
提示:求解函数方程以及求解其后问题时,令e10/3 - 1=2a,可便于计算分析处理。
(2)求出函数y=f(x)的一阶导数:dy/dx=f' (x)=?及其可导区域{x}=?
(3)给出函数y=f(x)的图像草图.
提示:①首先,寻找出函数f(x)的三个“零点”:xk=?[其中,f(xk )=0;(k=1,2,3)],以及一阶导数函数f'(x)的两个“零点”:xl'=?[其中,f' (xl' )=0;(l=1,2)].
②然后,考察函数f(x)的渐近性质.
③最后,利用①②的结果,便可绘制出函数f(x)的图像草图
[注意:“零点”方程f(xk )=0最终可化为关于xk的三次方程,可采用(分组分解法)因式分解后再作求解].

