大学数学-考研试题(理工数学Ⅰ 1987年矩阵的四则运算)

计算题（1987年理工数学Ⅰ）

设矩阵A和B满足关系式AB=A+2B，其中A=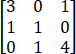，求矩阵B.

答案解析

由AB=A+2B，有(A-2E)B=A，于是

B=(A-2E)^-1A=

==.

讨论

矩阵的运算

设A=,A11∈Cr×r,rankA11=r且rankA=rankA11，证明：(1) A22-A21 A11-1 A12=0(2) N()=R()其中N(T),R(T)分别表示T∈Cm×n的零空间与列空间，即N(T)={x|Tx=0}⊂Cn R(T)={y|y=Tx,x∈Cn}⊂Cm Cm×n表示 m×n复数矩阵空间，Cn表示复n维列向量构成的线性空间，In-r表示 (n-r)×(n-r)单位矩阵。

设A∈Rm×n,rankA=r，证明存在可逆矩阵M∈Rm×m及正交矩阵P∈Rn×n，使得MAP= 其中Rm×n表示 m×n实数矩阵空间，Ir表示r×r单位矩阵，C∈Rr×(n-r)。

已知矩阵：A=,B=,C= 计算：(cosα∙A+cosβ∙B+cosγ∙C)3=？其中，cos2 α+cos2 β+cos2 γ=1,cosα+2cosβ+3cosγ=√3/3.提示：设E=，并引入三个矩阵：A'=A-E,B'=B-2E,C'=C-3E [注意：(cosα∙A'+cosβ∙B'+cosγ∙C')2=？]后，再作计算.

设A=,B=且A与B相似.(1)求α,β的值;(2)求可逆阵P使P-1 AP=B.

若x=(-1,2,3,0,4)，求‖x‖1,‖x‖2,‖x‖∞.

设A是n阶矩阵，A*为A的伴随矩阵，证明秩R(A*)与R(A)之间满足R(A* )=

设A≠0，证明：R(A)=1的充要条件是A可表示为一个列向量与一个行向量的乘积。

设A是一个n×n实矩阵，秩(A)=1，证明A2=kA，其中k为一实数.

设C=，求C101.

设A=(aij)是n阶实对称正定矩阵，b1,b2,…,bn为任意非零实数，证明B=(aijbibj)也是正定的。

矩阵

设S1,S3为实对称矩阵，S2为实矩阵，则矩阵S=为正定矩阵的充要条件为矩阵S3与矩阵S1-S2 S3-1 S2'皆为正定矩阵。

设A为实对称矩阵。证明当实数t充分大之后，tI+A是正定矩阵，其中I表示单位矩阵。

设A,B,C,D都是n×n矩阵，且|A|≠0,AC=CA，证明=|AD-CB|.

设A=(aij)n×n为正定矩阵.证明：f(x1,x2,…,xn )=是负定二次型，其中符号|∙|表示行列式.

设A=为n×n正定矩阵，证明：|A|≤a11 a22…ann.其中符号|∙|表示行列式.

设A=,A*为A的伴随矩阵，则|(1/4 A)-1 - 15A* |=________.

设A是n阶正定矩阵，B为n阶实方阵，证明：(1)若B'=B,则AB的特征值为实数；(2)若B正定,则AB的特征值皆大于0；(3)若B正定,且AB=BA,则AB正定。

设A为正交阵，且A|=-1，证明：A+E不可逆.

设A,B均为n阶实对称阵，A的特征值均小于a，B的特征值均小于b.证明：对任意的k>a+b,A+B-kE是负定矩阵.

设A是n级实对称矩阵，证明rank(A)=n的充要条件是：存在实对称矩阵B使AB+B'A是正定矩阵。

矩阵的四则运算

方阵A=，而n≥2为整数，则A2-2An-1=__________。

已知A=,B=满足(E-A-1B) XT=A-1（其中E为单位阵），试求X。

考虑循环矩阵A=证明：(1) A=a0 In+a1 T+a2 T2+⋯+an-1 Tn-1，其中T=In表示n×n单位矩阵。(2) T相似于对角矩阵。(3) A相似于对角矩阵。

设B为一r×r矩阵，C为一r×n矩阵.如果BC=C,问B=E是否成立？若成立，证明之；若不成立，举出反例，并给出使B=E的充要条件。其中E为单位矩阵.

已知A=,B为三阶方阵，满足A2B=A+AB，求B。

设A,A-E可逆，若B满足(E-(A-E)-1 )B=A，则B-A=______________.

设3阶方阵A,B满足关系式A-1BA=6A+BA，且A=，则B=____________.

已知α=[1,2,3],β=[1,1/2,1/3]，设A=αTβ，其中αT是α的转置，则An=________________.

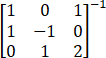
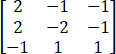
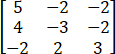设n阶方阵A,B,C满足关系式ABC=E，其中E是n阶单位矩阵，则必有【】

已知AP=PB，其中B=,P=，求A,A5.