设A=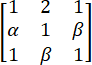
,B=
且A与B相似.
(1)求α,β的值;
(2)求可逆阵P使P-1 AP=B.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设A是n阶矩阵，A*为A的伴随矩阵，证明秩R(A*)与R(A)之间满足R(A* )=
设A为任一n阶矩阵，数λ>0，证明λI+AT A为正定矩阵。
设A≠0，证明：R(A)=1的充要条件是A可表示为一个列向量与一个行向量的乘积。
方阵A=，而n≥2为整数，则A2-2An-1=__________。
已知A=,B=满足(E-A-1B) XT=A-1（其中E为单位阵），试求X。
设A为m×n且秩为s的矩阵，X为p×m的列满秩矩阵，即r(X)=m，而Y为n×q的行满秩矩阵，即r(Y)=n。证明：r(A)=r(XA)=r(AY)=r(XAY)其中符号r(T)表示矩阵T的秩。
证明：任一可逆的实矩阵A可以表示成A=QB，其中Q为正交矩阵，B是主对角线上元素均为正的三角形矩阵：B=,bii>0,且此表示式是惟一的。
考虑循环矩阵A=证明：(1) A=a0 In+a1 T+a2 T2+⋯+an-1 Tn-1，其中T=In表示n×n单位矩阵。(2) T相似于对角矩阵。(3) A相似于对角矩阵。
设矩阵T=,T以及D可逆，证明(A-BD-1 C)-1存在，并求T-1，其中A,B,C,D为适当维度的矩阵。
设矩阵A=仅有两个不同的特征值.若A相似于对角矩阵，求a,b的值，并求可逆矩阵P，使P-1AP为对角矩阵.
设A=E-ξξT，其中E是n阶单位矩阵，ξ是n维非零列向量，ξT是ξ的转置，证明：(1)A2=A的充要条件是ξTξ=1;(2)当ξTξ=1时，A是不可逆矩阵.
设A是n阶可逆方阵，将A的第i行和第j行对换后得到的矩阵记为B.(1)证明B可逆；(2)求AB-1.
设A为方阵，g(λ)是A的最小多项式，f(λ)为任意多项式.证明：f(A)可逆⇔(f(λ),g(λ))=1.
设4阶方阵A=，则A的逆矩阵A-1=____________.
设矩阵A=,E=，则逆矩阵(A-2E)-1=________.
设A∈Rm×n,rankA=r，证明存在可逆矩阵M∈Rm×m及正交矩阵P∈Rn×n，使得MAP= 其中Rm×n表示 m×n实数矩阵空间，Ir表示r×r单位矩阵，C∈Rr×(n-r)。
设A=(aij)是n阶实对称正定矩阵，b1,b2,…,bn为任意非零实数，证明B=(aijbibj)也是正定的。
设α1,…,αn和β1,…,βn是线性空间V的两组基，V上的线性变换A把每个αi映成βi,i=1,…,n.证明：A在α1,…,αn下的矩阵和在β1,…,βn下的矩阵相等.
已知A=(1) 求正交矩阵P，使得PTAP为对角矩阵；(2) 求正定矩阵C，使得C2 = (a+3)E-A.
设=QR，其中Q是正交方阵，R是对角线元素大于0的上三角方阵，则R=________.
设4阶矩阵B=,C=，且矩阵A满足关系式A(E-C-1 B)T CT=E,其中E为4阶单位矩阵，C-1表示 C的逆矩阵，CT表示 C的转置矩阵，将上述关系式化简并求矩阵A.