设A=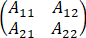 ,A11∈Cr×r,rankA11=r且rankA=rankA11,证明:
,A11∈Cr×r,rankA11=r且rankA=rankA11,证明:
(1) A22-A21 A11-1 A12=0
(2) N(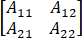 )=R(
)=R(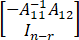 )
)
其中N(T),R(T)分别表示T∈Cm×n的零空间与列空间,即
N(T)={x|Tx=0}⊂Cn
R(T)={y|y=Tx,x∈Cn}⊂Cm
Cm×n表示 m×n复数矩阵空间,Cn表示复n维列向量构成的线性空间,In-r表示 (n-r)×(n-r)单位矩阵。
设A=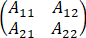 ,A11∈Cr×r,rankA11=r且rankA=rankA11,证明:
,A11∈Cr×r,rankA11=r且rankA=rankA11,证明:
(1) A22-A21 A11-1 A12=0
(2) N(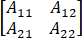 )=R(
)=R(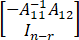 )
)
其中N(T),R(T)分别表示T∈Cm×n的零空间与列空间,即
N(T)={x|Tx=0}⊂Cn
R(T)={y|y=Tx,x∈Cn}⊂Cm
Cm×n表示 m×n复数矩阵空间,Cn表示复n维列向量构成的线性空间,In-r表示 (n-r)×(n-r)单位矩阵。
暂无答案
设A是n阶矩阵,A*为A的伴随矩阵,证明秩R(A*)与R(A)之间满足R(A* )=
设A≠0,证明:R(A)=1的充要条件是A可表示为一个列向量与一个行向量的乘积。
设A为m×n且秩为s的矩阵,X为p×m的列满秩矩阵,即r(X)=m,而Y为n×q的行满秩矩阵,即r(Y)=n。证明:r(A)=r(XA)=r(AY)=r(XAY)其中符号r(T)表示矩阵T的秩。
设A是4×3矩阵,且A的秩r(A)=2,而B=,则r(AB)=________.
设A,B都是n(n≥2)阶复方阵,则rank(AB)=rank(BA).
已知n阶矩阵A,B,C满足ABC=0,E是n阶单位矩阵,记矩阵,,的秩分别为γ1,γ2,γ3,则【 】
若x=(-1,2,3,0,4),求‖x‖1,‖x‖2,‖x‖∞.
设A=,则A-1=__________,A2022=__________,A的最大奇异值σ1=__________.
已知A=(1) 求正交矩阵P,使得PTAP为对角矩阵;(2) 求正定矩阵C,使得C2 = (a+3)E-A.
设A=(aij)是n阶实对称正定矩阵,b1,b2,…,bn为任意非零实数,证明B=(aijbibj)也是正定的。
设A为任一n阶矩阵,数λ>0,证明λI+AT A为正定矩阵。
方阵A=,而n≥2为整数,则A2-2An-1=__________。
已知矩阵A=,若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵,则P,Q可以分别取【 】
设A,B为n阶可逆矩阵,E为n阶单位矩阵,M*为M的伴随矩阵,则=【 】
设A,B,C,D都是n×n矩阵,且|A|≠0,AC=CA,证明=|AD-CB|.
给定方程x''+8x'+7x=f(t),其中f(t)在(-∞,+∞)上连续。如果f(t)=0,则上述方程的每一个解当t→+∞时都趋于零。
设A=(aij)n×n,且行列式≠0,1≤k≤n.证明存在下三角形矩阵Bn×n,使BA为上三角形矩阵。
设a1,a2,⋯,an是n个实数,都落在区间(-1,1)里.(1)证明 ∏1≤i,j≤n(1+aiaj)/(1-aiaj )≥1(2)找出以上不等式中等号成立的充分必要条件.